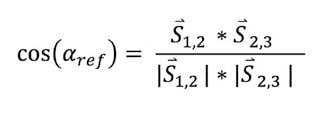Zwei Segmente eines mechanischen Modells mit je einem Inertialsensor (IMU) wurden über ein Scharniergelenk miteinander verbunden. Die Rotationsachse und die Sensororientierung wurden per Ultraschall-Positionssystem in 50 zufälligen Ausrichtungen extern und mit dem neuen Verfahren bestimmt. Somit konnte die mittels IMU berechnete Achse durch ein externes Referenzsystem überprüft werden. Der Vergleich der Methoden erfolgte über eine Bland-Altman- Statistik, eine lineare Regression und eine Intra-Klassen-Korrelation. Eine mittlere Abweichung vom Referenzsystem von ‑0.13° und ein Korrelations-Koeffizient von r = .99 belegen die Validität des Verfahrens. Das neue System erlaubt eine ökonomische und präzise Bestimmung der Orientierung der unteren Sprunggelenkachse.
Einleitung
Die Kenntnis der Ausprägung individueller anatomischer Strukturen ist Grundlage spezifischer Präventions-und Behandlungsstrategien. Die Bedeutung der unteren Sprunggelenkachse im Kontext akuter und chronischer Überlastungen des Fußes wurde in der Literatur bereits häufig diskutiert 123456. Der gemeinsame Ansatz war neben der „Schrägheit“ 7 der Achse immer die „außerordentliche Varianz“ 8 der anatomischen Strukturen. Bereits Ende der 60er Jahre stellte Isman fest: „[T]he variation in the positions of the different axes is such that they require individual determination“ 9. Die Projektion der unteren Sprunggelenkachse auf die Transversalebene veranschaulicht die Relevanz der Orientierung der unteren Sprunggelenkachse. Das aufgebrachte Moment der invertorisch und evertorisch wirkenden Muskeln kann durch einen vergrößerten senkrechten Abstand zur Rotationsachse erhöht werden. Im Falle des M. tibialis anterior beispielsweise ist das aufgebrachte stabilisierende Moment bei erhöhter Abweichung von der sagittalen Ebene des Fußes verringert. Der gesamte Sprunggelenk-Komplex besteht aus dem oberen und dem unteren Sprunggelenk. Die Achsen der Sprunggelenke liegen nicht orthogonal aufeinander, wodurch es zu einer Bewegungsfusion beider Gelenke kommt. Alt (2001) 8und nachfolgend Hochwald (2007) 10sowie Lewis et al. (2007) 11zeigten, dass für eine funktionelle Diagnostik der unteren Sprunggelenkachse der Talus durch eine maximale Dorsalflexion zwischen den Trochlea der Tibia eingeklemmt und als bewegungsunfähig angesehen werden kann.
Unter dieser Voraussetzung kann zur Bestimmung der anatomischen Achse des unteren Sprunggelenks die Bewegung als monoaxial vereinfacht aufgefasst. Bislang fehlt es allerdings an diagnostischen Verfahren, die die Orientierung der Rotationsachse im Kontext alltäglicher Anwendung ökonomisch und hinreichend genau bestimmen. Herkömmliche Bewegungsanalysesysteme mit reflektierenden Markern und anatomischen Punkten sind aufgrund der Rolle des Talus, dessen Bewegung an der Hautoberfläche nicht beobachtbar ist, problematisch. Bildgebende Verfahren (MRT, Röntgen) sind zeitlich sehr aufwendig, teuer, nicht portabel und – im Falle von Röntgenaufnahmen – wegen des invasiven Charakters ethisch bedenklich. Außerdem stehen die Informationen über die Orientierung der Rotationsachsen erst nach aufwendiger Verarbeitung der Daten zur Verfügung. Weiterhin lassen Ergebnisse aus der Arbeit von Nichols et al. (2017) 12 vermuten, dass statisch bestimmte Rotationsachsen nur geringe funktionelle Relevanz besitzen. Daher sollten dynamische Messungen durchgeführt werden. Es existieren unterschiedliche Angaben über die Freiheitsgrade des unteren Sprunggelenks 891213. Die Mehrheit der Autoren geht nach Alt (2001, S. 60) 8 von einer monoaxialen Gelenkbewegung in einem Freiheitsgrad aus. Unter dieser modellhaften Annahme lässt sich die Rotation benachbarter Segmente um die gemeinsame Achse nach Seel et al. (2012) 14 mathematisch durch die Winkelgeschwindigkeiten beider Segmente beschreiben. Winkelgeschwindigkeiten können über inertiale Messeinheiten (IMU) bestimmt werden. Ziel der Studie ist die Überprüfung eines Algorithmus zur Bestimmung von Rotationsachsen für dessen Einsatz in einem diagnostischen Verfahren für den klinischen Alltag.
Inertialsensoren zur Bestimmung der Gelenkkinematik
Miniaturisierte Sensoren erfassen Beschleunigungen, Drehraten und magnetische Flussdichten zur Bestimmung der Sensororientierung im Trägheitssystem Erde. Im Vergleich zu etablierten Markersystemen sind IMUbasierte Systeme kostengünstiger und portabel. Die geringeren technologischen Anforderungen ermöglichen Einsätze in Felduntersuchungen. Die wesentlichen Probleme beim Einsatz der IMUs bestehen in zeitabhängigen Stabilitätsproblemen der Messdaten: Winzige Ungenauigkeiten in der Herstellung der mikromechanischen Systeme führen zu Driftverhalten, besonders der Drehratensensoren. Außerdem ist mathematisch eine doppelte Integration der Beschleunigung nötig, um die Position im Raum zu bestimmen. Im zeitlichen Verlauf der Daten summieren sich die Messfehler zunehmend auf, und die Genauigkeit der Messdaten verringert sich. Zudem können elektromagnetische Störfelder die Genauigkeit der Sensordaten verringern. Die jüngste Literatur zeigt aber, dass mit Verfahren zur Bestimmung menschlicher Kinematik unter Verwendung von IMUs 15161718 die Genauigkeit markerbasierter Systeme annähernd erreicht werden kann. Dabei wurden auch mathematische Verfahren vorgestellt, welche die Rotationsachen zwischen angrenzenden Sensoren bestimmen 1920.
Das in der vorliegenden Arbeit validierte Modell zeichnet sich durch die folgenden Eigenschaften aus:
- Die Berechnung kommt ohne Integration der Messdaten aus.
- Es sind keine Kalibrierungs- verfahren im Vorfeld nötig.
- Die Orientierung der Sensoren zueinander kann zufällig gewählt werden.
- Der Algorithmus ist zur Online- Verarbeitung geeignet und ermöglicht eine direkte Darstellung der Ergebnisse.
Damit sind die Voraussetzungen für ein im klinischen Alltag einsetzbares diagnostisches System gegeben.
Material und Methoden
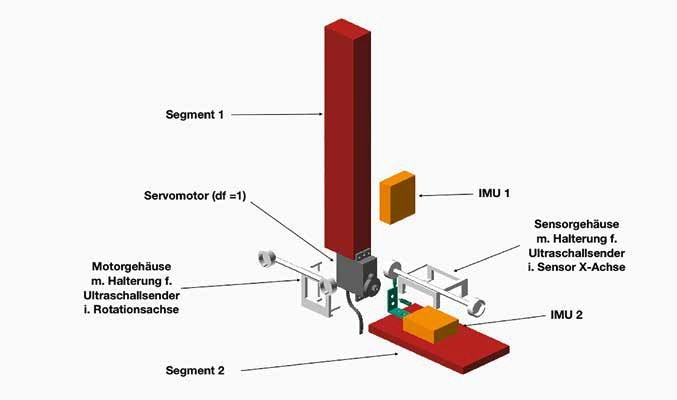
Das Verfahren wurde anhand eines mechanischen Modells überprüft. Zwei Segmente wurden durch ein Scharniergelenk miteinander verbunden. Die Rotationsbewegungen wurden durch einen Servomotor im Gelenk erzeugt. Der Servomotor wurde über ein Arduino-Leonardo-Mikrocontroller- Board betrieben und über eine in Matlab® 2019a geschriebene Nutzeroberfläche gesteuert, um unterschiedliche Bewegungsumfänge, ‑geschwindigkeiten und ‑formen reproduzierbar zu testen. Auf die Segmente wurde je ein IMU der Firma Xsens (MTw Awinda) in zufälliger Ausrichtung angebracht. Die Winkelgeschwindigkeiten wurden in drei orthogonalen Achsen mit 50 Hz Abtastrate aufgezeichnet.
Zur Transformation der IMU-Daten in ein Laborkoordinatensystem wurden Rotationsachse sowie Sensororientierung per Ultraschall-Positionssystem (Zebris CMS-20) bestimmt. Vier Ultraschallsender (S1– S4) wurden jeweils in Verlängerung der Sensor-x-Achse und der Rotationsache des Servomotors befestigt; die Aufnahmefrequenz betrug 120 Hz. Dazu wurden Verschalungen im 3D-Druckverfahren konstruiert (Abb. 1). In einer statischen Aufnahme über ca. 5 Sekunden wurde durch das CMS-20 die Position der Sender bestimmt. Die Sender werden als dreidimensionale Vektoren dargestellt, deren Ursprung im lokalen Koordinatensystem des CMS-20 liegt, das gleichzeitig als Laborkoordinatensystem definiert wurde. Die Sender S1 bis S4 bildeten die Vektoren der Form:
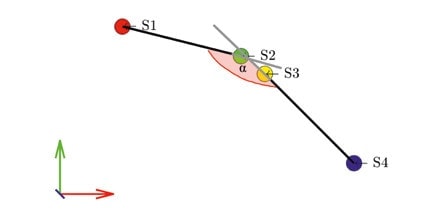
Die Orientierung der Sensor-x-Achse und der Rotationsachse wurden durch die Vektoren zwischen den Sendern S1 bis S4 wie in Abbildung 2 dargestellt berechnet. Das kinematische Modell nach Seel et al. (2012) 14 verlangt gelenkbeschreibende Winkelgeschwindigkeiten zur Berechnung der Rotationsachse. Eine entsprechende Berechnungsfunktion wurde in Matlab® 2019a implementiert und für die Sensordaten aus dem IMU-System modifiziert. Zusammengefasst wurden vier Parameter einer Funktion im iterativen Vorgehen angepasst, sodass das Ergebnis der Funktion minimal wird. Die berechnete Rotationsachse liegt im Sensor i ebenfalls in der Form
vor und hat die Länge 1. Dieser Vektor wird im lokalen Koordinatensystem der Sensoren ausgedrückt. Er spannt zusammen mit dem x‑Achsen-Vektor des Ursprungskoordinatensystems des IMUs den Winkel ∂IMU auf. Im Idealfall gibt es keinen Unterschied zwischen ∂IMU und ∂ref. Die interne Validität einer Methode ist immer dann gegeben, wenn eine Veränderung der unabhängigen Variable eindeutig auf die Veränderung der abhängigen Variable zurückzuführen ist, im vorliegenden Fall also der Winkel zwischen Sensor und Rotationsachse. Die Abweichung der Sensor-x- Achse zur Rotationsachse des mechanischen Modells wurde daher 50 Mal mit wechselnder zufälliger Ausrichtung der IMUs bestimmt und mit den Ergebnissen aus den statischen CMS- 20-Messungen verglichen. Neben der grundlegenden Überprüfung des Berechnungsmodells ist die Robustheit des Algorithmus gegenüber Störfaktoren menschlicher Bewegung für spätere Anwendungen von zentraler Bedeutung. Es ist nicht anzunehmen, dass eine menschliche Bewegungsausführung ähnlich gleichförmig verläuft wie die eines Servomotors. Vielmehr kann angenommen werden, dass das Bewegungsausmaß im unteren Sprunggelenk interindividuell variiert, ebenso wie die Bewegungsgeschwindigkeit. Außerdem sind inertiale Sensorsysteme dafür bekannt, mit zunehmender Aufnahmezeit an Präzision zu verlieren 21. Daher wurden Aufnahmezeit, Bewegungsausmaß, Bewegungsgeschwindigkeit und Bewegungsausführung systematisch über den Motor variiert. Zur statistischen Absicherung der Ergebnisse wurden Bland-Altman- Plots 22 und eine lineare Regression verwendet. Zusätzlich wurden die Daten mittels Intra-Klassen-Korrelation auf absolute Übereinstimmung überprüft. Zur Quantifizierung des Unterschieds zwischen den Methoden wurde der „sum of squares error“ (SSE) berechnet.
Ergebnisse
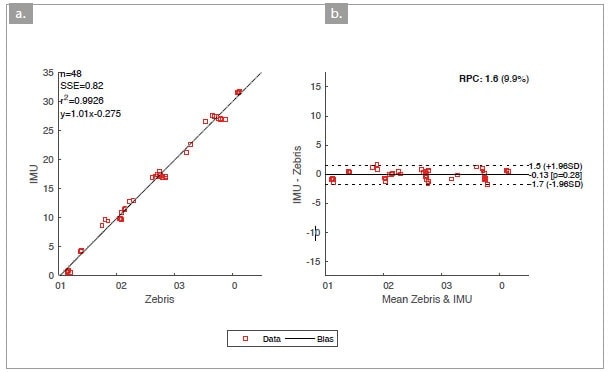
Aus den 50 Versuchen konnten 48 Datensätze ausgewertet werden. Die Bland-Altman-Statistik und die lineare Regression sind in Abbildung 3 dargestellt.
Diskussion
Ziel in der vorliegenden Arbeit war die Überprüfung eines Algorithmus zur Bestimmung von Rotationsachsen für den Einsatz in der alltäglichen klinischen Diagnostik. Die Ergebnisse zeigen, dass die Rotationsachse eines mechanischen Modells mit hoher Genauigkeit reproduzierbar berechnet werden kann. Die mittlere Abweichung der Achse mit ‑0.13° ist marginal und vernachlässigbar. Die Intra-Klassen-Korrelation mit r = .99 bedeutet eine fast optimale Übereinstimmung der Systeme. Zudem konnte gezeigt werden, dass die Bestimmung der Rotationsachse nicht durch Faktoren wie Aufnahmezeit, Bewegungsgeschwindigkeit, ‑ausmaß oder ‑form beeinflusst wird; der Algorithmus ist valide. Ein unmittelbarer Transfer vom mechanischen Modell auf das menschliche Sprunggelenk ist allerdings kritisch zu beurteilen: Wie bereits einige Arbeiten zeigten, wurde das untere Sprunggelenk nicht übereinstimmend als Gelenk mit einem Freiheitsgrad beschrieben. Es kann auch sein, dass es während der Rotationen im Gelenk zu Translationen entlang der Rotationachse kommt8. Da jedoch die Berechnung ausschließlich auf den Winkelgeschwindigkeiten basiert, sind Translationen entlang der Achse irrelevant und beeinflussen das Ergebnis nicht. Am mechanischen Modell ist der Sensor direkt mit dem „punctum mobile“ verbunden – im Gegensatz dazu werden die Segmentbewegungen beim Menschen an der Hautoberfläche gemessen. Relativbewegungen zwischen Haut und Knochen beeinflussen die Datenqualität. Betrachtet man die Hautverschiebungen als stochastischen Fehler, wird dessen Einfluss über die zunehmende Anzahl an Messdaten verringert. Zudem ist eine mögliche Bewegung des Talus trotz maximaler Dorsalflexion kritisch zu betrachten. Der funktionelle Zusammenhang mit der oberen Sprunggelenkachse wurde bei den Überlegungen in dieser Arbeit zunächst ignoriert; diese müssen bei der Interpretation der Orientierung der unteren Sprunggelenkachse jedoch mit einbezogen werden. Es bleibt zu klären, welche Bedeutung die Orientierung der oberen Sprunggelenkachse für die Funktionsweise des unteren Sprunggelenkes hat. Der bedeutendste Unterschied zwischen Modell und menschlichem Fuß ist die Gelenkmorphologie: Im menschlichen Fuß artikulieren konkave und konvexe Gelenkflächen miteinander. Eine Gelenkachse ist als latentes Konstrukt nicht direkt beobachtbar.
Die Orientierung der Achse des unteren Sprunggelenks wird üblicherweise mit den Winkeln „Deviation“ und „Inklination“ angegeben. Die Deviation ist die Abweichung von der Mittellinie des Fußes; die Inklination beschreibt die Abweichung der Transversalebene. Wie oben beschrieben werden die Rotationsachsen bislang ausschließlich in lokalen Sensor-Koordinatensystemen angegeben. Die einfachste Möglichkeit eines gemeinsamen Bezugssystems wäre die kongruente Orientierung der jeweiligen Koordinatensysteme. Eine exakte Ausrichtung der Sensoren am Segment ist praktisch nicht möglich. Die Eigenschaften des Algorithmus machen es daher erforderlich, die ermittelten Rotationsachsen in ein allgemeingültiges Koordinatensystem zu überführen. Ein sinnvoller interindividueller Vergleich wäre nur durch die Kenntnis der Orientierung der Sensoren in Bezug auf die jeweiligen anatomischen Strukturen möglich. Daher wurde ein zusätzliches Kalibrierungsverfahren entwickelt und validiert, das die Rotationsachse in ein personenspezifisches Koordinatensystem übersetzt. Durch die hohe Genauigkeit, die einfache Anwendung und die direkte Rückmeldung ist das vorgestellte Verfahren für den klinischen Alltag geeignet. Es eröffnet die Möglichkeit einer individualisierten Diagnostik als Grundlage spezifischer Präventions-und Behandlungsstrategien.
Ausblick
Mit dem vorgestellten Verfahren ist es erstmals möglich, die Orientierung der unteren Sprunggelenkachse genauer zu schätzen. Hieraus ergibt sich eine Reihe möglicher Fragestellungen und Anwendungsgebiete, sowohl für die Forschung als auch für den orthopädischen Alltag. Lersch et al. (2012) 23 fürdern beispielsweise den Einbezug der Fußkinematik in die klinische Diagnostik, die maßgeblich von der Orientierung der Rotationsachsen abhängt. Des Weiteren könnten die Rotationsachsen zukünftig als zusätzliches Kriterium für die individuelle Schuhgestaltung bei pathologischen Füßen dienen. In der Ausrüstung mit orthopädischen Gang- und Stabilitätshilfen könnte die Orientierung der Achse einbezogen werden, um individualisierte Rückstellmomente zu erzeugen. In der klinischen Forschung wird es von vorrangigem Interesse sein, ob die Orientierung der unteren Sprunggelenkachse und die daraus abgeleiteten Momente im Gelenk relevant für die Ausbildung chronischer Überlastungen – insbesondere der Achillessehne – sein können.
Für die Autoren:
Sascha Schlechtweg
Institut für Sport- und Bewegungswissenschaft Universität Stuttgart
Allmandring 28
70569 Stuttgart
sascha.schlechtweg@inspo.uni-stuttgart.de
Begutachteter Beitrag/reviewed paper
Schlechtweg S, Hauser E‑H, Alt W. Der Einsatz inertialer Sensorik zur Bestimmung individueller Rotationsachsen im unteren Sprunggelenk. Orthopädie Technik. 2019; 70 (12): 25–29
- Kinder mit Trisomie 21: Einsatz der Ganganalyse zur adäquaten Schuh- und Orthesenversorgung — 5. November 2024
- Rehabilitation aus orthopädietechnischer und physiotherapeutischer Sicht – Osseointegration und Schaftprothesen der unteren Extremität im Vergleich — 5. November 2024
- Belastungsprofile von knochenverankerten Oberschenkelimplantaten verbunden mit modernen Prothesenpassteilen — 5. November 2024
- Alt W. Biomechanische Aspekte der Gelenkstabilisierung
– dargestellt am Beispiel des Sprunggelenks. Geislingen (Steige): Maurer, 2001 - Alt WW, Meinert I, Weh J, Reule CA. The concept of joint axes and its application to the joints of the ankle. Footwear Sci, 2013; 5 (Suppl. 1): 9–11. doi:10.1080/194 24280.2013.797932
- McClay I, Bray J. The subtalar angle: a proposed measure
of rearfoot structure. Foot Ankle Int, 1996; 17 (8): 499–502 - Piazza SJ. Mechanics of the Subtalar Joint and Its Function During Walking. Foot Ankle Clin, 2005; 10:
425–442. doi:10.1016/j.fcl.2005.04.001 - Lewis GS, Cohen TL, Seisler AR, Kirby KA, Sheehan FT, Piazza SJ. In vivo tests of an improved method
for functional location of the subtalar joint axis. J Biomech, 2009; 42 (2): 146–151. doi:10.1016/j.jbiomech. 2008.10.010 - van den Bogert A, Smith G. In vivo Determination of the Ankle Joint Complex: an Optimization Approach. J Biomech, 1994; 27 (12): 1477–1488. doi: 10.1016/0021–9290(94)90197‑X
- McClay I, Bray J. The subtalar angle: a proposed measure of rearfoot structure. Foot Ankle Int, 1996; 17 (8): 499–502
- Alt W. Biomechanische Aspekte der Gelenkstabilisierung – dargestellt am Beispiel des Sprunggelenks. Geislingen (Steige): Maurer, 2001
- Isman R, Inman V, Poor P. Anthropometric studies of the human foot and ankle. Bull Prosthet Res, 1969; 11: 97–129. doi:10.1007/s11695-014‑1382‑z
- Hochwald H. Entwicklung eines diagnostischen Verfahrens zur Bestimmung der Gelenkachsen des Sprunggelenks. Dissertation, Universität Stuttgart, 2007. http://dx.doi.org/10.18419/opus-5479 (Zugriff am 21.11.2019)
- Lewis GS, Kirby KA, Piazza SJ. Determination of subtalar joint axis location by restriction of talocrural joint motion. Gait Posture, 2007; 25 (1): 63–69. doi:10.1016/j.gaitpost.2006.01.001
- Nichols JA, Roach KE, Fiorentino NM, Anderson AE. Subject-Specific Axes of Rotation Based on Talar Morphology Do Not Improve Predictions of Tibiotalar and Subtalar Joint Kinematics. Ann Biomed Eng, 2017; 45 (9): 2109–2121. doi:10.1007/s10439-017‑1874‑9
- Lundberg A, Svensson OK. The axes of rotation of the talocalcaneal and talonavicular joints. Foot, 1993; 3 (2): 65–70. doi:10.1016/0958–2592(93)90064‑A
- Seel T, Schauer T. Joint Axis and Position Estimation from Inertial Measurement Data by Exploiting Kinematic Constraints. In: IEEE Multi-Conference on Systems and Control, 2012: 0–4
- Seel T, Raisch J, Schauer T. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors, 2014; 14 (4): 6891–6909. doi:10.3390/s140406891
- McGrath T, Fineman R, Stirling L. Correction: An auto-calibrating knee flexion-extension axis estimator using principal component analysis with inertial sensors (Sensors, 2018; 18 (6): 1882). Sensors (Switzerland), 2018; 19 (7). doi:10.3390/s19071504
- Laidig D, Müller P, Seel T. Automatic anatomical calibration for IMU- based elbow angle measurement in disturbed magnetic fields. Curr Dir Biomed Eng, 2017; 3 (2): 167–170. doi:10.1515/cdbme-2017–0035
- Laidig D, Schauer T, Seel T. Exploiting kinematic
constraints to compensate magnetic disturbances when calculating joint angles of approximate hinge joints from orientation estimates of inertial sensors. IEEE International Conference on Rehabilitation Robotics, 2017. doi:10.1109/ICORR.2017.8009375 - McGrath T, Fineman R, Stirling L. Correction: An
auto-calibrating knee flexion-extension axis estimator using principal component analysis with inertial sensors (Sensors, 2018; 18 (6): 1882). Sensors (Switzerland), 2018; 19 (7). doi:10.3390/s19071504 - Seel T, Schauer T. IMU-based Joint Angle Measurement Made Practical. Proc Tech Assist, 2012: 6.
- Chen P, Oelmann B. Joint-Angle Measurement Using Accelerometers and Gyroscopes – A Survey. IEEE Transactions on Instrumentation and Measurement, 2010; 59 (2): 404–414. doi:10.1109/TIM.2009.2024367
- Bland U, Giavarina D. Understanding Bland Altman analysis. Biochem Med (Zagreb), 2015; 25 (2): 141–151
- Lersch C, Grötsch A, Segesser B, Koebke J, Brüggemann
GP, Potthast W. Influence of calcaneus angle and muscle forces on strain distribution in the human Achilles tendon. Clin Biomech, 2012; 27 (9): 955–961. doi:10.1016/j.clinbiomech.2012.07.001