Einleitung
Die Hauptfunktion orthetischer Systeme besteht in der Förderung der Mobilität der Anwender, indem sie beeinträchtigte biomechanische Fähigkeiten des menschlichen Körpers wiederherstellen beziehungsweise substituieren. Daher sind bei der Entwicklung solcher Systeme Kenntnisse über die zu unterstützende Bewegung substanziell wichtig. Die Dynamik der zu unterstützenden Bewegung kann im Vorfeld prinzipiell rein messtechnisch analysiert werden, und zwar unter Nutzung verschiedener Methoden der Kraftmessung, der Kinematografie (Motion Capture) oder der Messung muskulärer Aktivität (Elektromyografie) 1. Simulationsbasierte Methoden bieten in diesem Zusammenhang jedoch mehrere Vorteile wie Verzicht auf den Bau von Prototypen, mehr Variationsmöglichkeiten, höhere Zeit- und Ressourceneffizienz und anderes. Neben der als selbstverständlich vorausgesetzten Qualität der Simulationsergebnisse ist die Synthesefreundlichkeit eine wichtige Voraussetzung dafür. Diese manifestiert sich in kurzen Rechenzeiten, flexibler Parametrierung, einfacher Kommunikation mit Konstruktionssoftware und Unterstützung der Entwicklungslogik.
Im Rahmen der hier vorgestellten Studie wird die Software “AnyBody Modeling System™” (AMS) eingesetzt, die diesbezüglich relativ günstige Eigenschaften aufweist 2 3. Mit dieser Software können in frühen Entwurfsphasen funktionelle oder prinzipielle Lösungen orthetischer Systeme funktionell abgesichert und strukturell optimiert werden, beispielsweise durch Variation geometrischer Anordnungen der Unterstützungselemente oder deren Kraftverläufe, bedingt durch Federkonstanten und Vorspannungen.
In diesem Beitrag wird die unterstützende Wirkung eines aktiven Elementes (motorgetriebener Seilzug) und zwei verschiedener passiver Elemente (Federn) eines Bewegungsunterstützungssystems (BUS) bei der Treppenüberwindung analysiert. Exemplarisch wird dabei der Treppenaufstieg eines Menschmodells, basierend auf gemessenen Daten, gemeinsam mit den Unterstützungselementen simuliert.
Methodisches Vorgehen
Messung kinematischer und kinetischer Daten des Treppenaufstieges
Zur simulativen Untersuchung orthetischer Teilsysteme werden kinematische und kinetische Daten des Treppenaufstieges benötigt. Die für die Simulation verwendeten Daten entstammen einer biomechanischen Studie zur Treppenüberwindung, wobei für die Simulation der orthetischen Teilsysteme in diesem Beitrag die Daten eines männlichen Probanden (23 Jahre) mit durchschnittlichen Körperabmessungen verwendet wurden. Die Messung erfolgte an einer vierstufigen Treppe mit Normabmessungen (Stufenhöhe:160 mm; Auftritt: 280 mm) nach 4 und einem Steigungswinkel von 30°. Für die Erfassung der kinetischen Eingangsgrößen wurde eine Kraftmessplatte (MiniDyn Typ 9119AA2, Kistler, Winterthur, Schweiz) in der zweiten Stufe verwendet. Des Weiteren wurden die Körpergröße (1,78 m), die Masse (79,4 kg) und die jeweiligen Segmentlängen (Oberschenkellänge: 0,462 m; Unterschenkellänge: 0,384 m; Fußlänge: 0,265 m) gemessen.
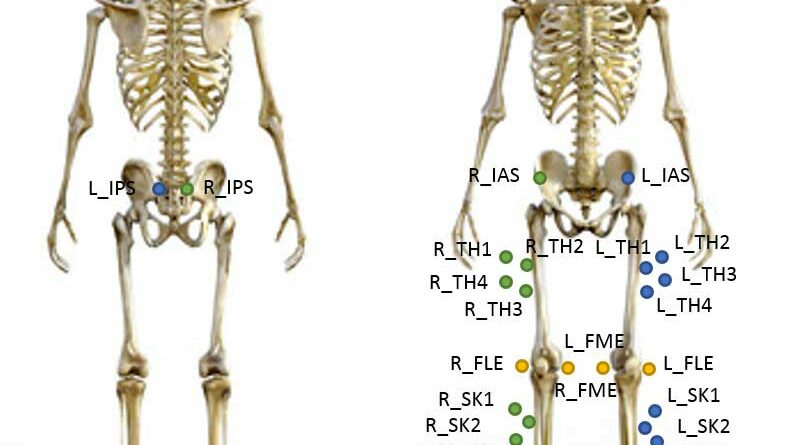
Für die kinematischen Daten wurde ein markerbasiertes Bewegungsaufnahmesystem (Qualisys AB, Göteborg, Schweden), bestehend aus zwölf aktiven im Raum verteilten Infrarotkameras, verwendet. Basierend auf dem Cast-Modell 5 (Abb. 1 u. 2) und der Ergänzung zweier Marker an der Schulter wurden insgesamt 36 passive Infrarotmarker angebracht; zusätzlich wurden für die statische Aufnahme zur Bestimmung der Gelenkachsen und Segmentlängen weitere acht Marker medial und lateral am Knie- und Fußgelenk beider Beine befestigt. Die Datenaufnahme der Kinematik erfolgte mit 100 Hz, die der Kinetik mit 500 Hz. Zur Aufnahme und Synchronisation wurde die Software “Qualisys Track Manager” verwendet. Lücken in den Trajektorien wurden durch Interpolation vervollständigt, wobei maximal zehn zusammenhängende Frames ergänzt wurden.
Erstellung des Simulationsmodells
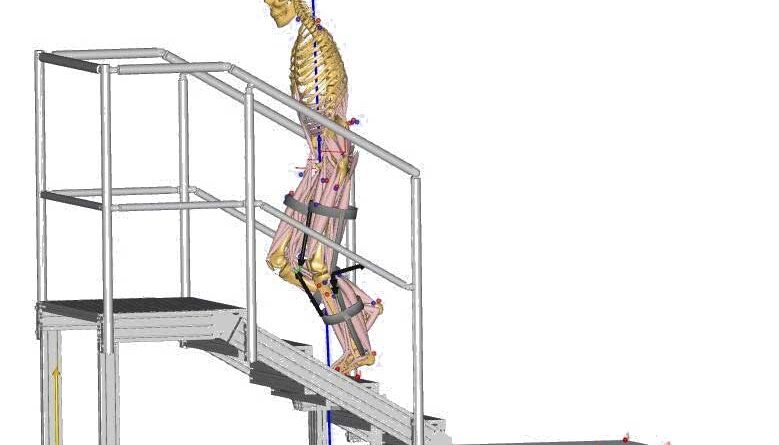
Das Simulationsmodell besteht aus dem Modell des Menschen und den orthetischen Teilsystemen des Bewegungsunterstützungssystems. Verwendet wurde das Menschmodell von AMS (Abb. 3) ohne Arme mit 36 Segmenten. Die Modellierung des unteren Bewegungsapparates basiert auf 6. Eine Skalierung des Modells ist unter Berücksichtigung von Masse, Körpergröße und Fettanteil möglich 7.
Somit wurden die vorher gemessene Körpermasse, die Körpergröße sowie die Segmentlängen entsprechend berücksichtigt. Die Gelenkzentren der Hüfte wurden nach 8 geschätzt, wobei die Distanz der Gelenkzentren demnach 0,17 m beträgt.
Das Bewegungsunterstützungssystem (BUS) wird als geometrisches und masseloses Modell aus zwei Teilen generiert und in AMS implementiert. Die Masse des BUS wird aufgrund der gemessenen Bodenreaktionskräfte ohne BUS nicht berücksichtigt. Die virtuelle Anbindung der beiden Teile untereinander erfolgt durch ein Rotationsgelenk, das kongruent zur Kniegelenksachse des Menschmodells ist. Des Weiteren erfolgt eine starre Anbindung der beiden Teile jeweils am Femur und an der Tibia.
Implementierung der kinematischen und kinetischen Daten
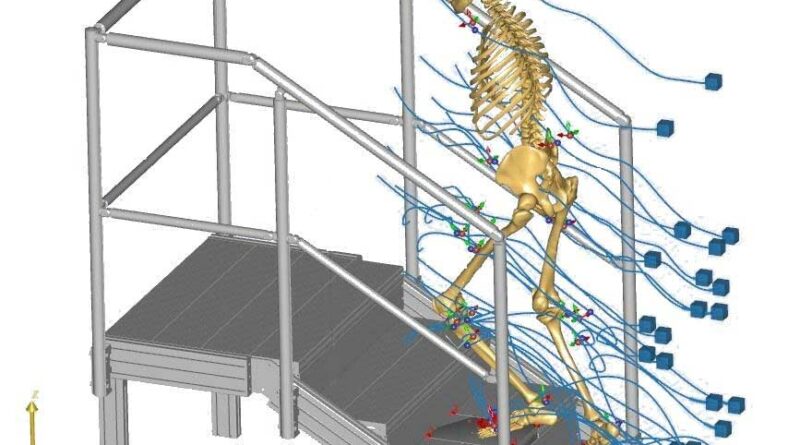
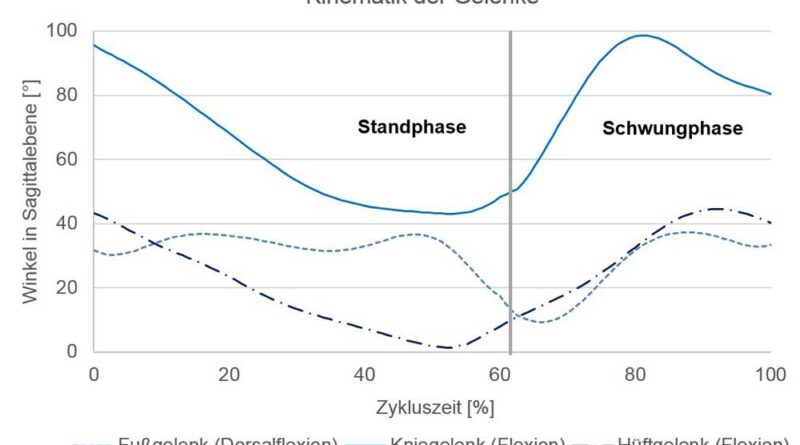
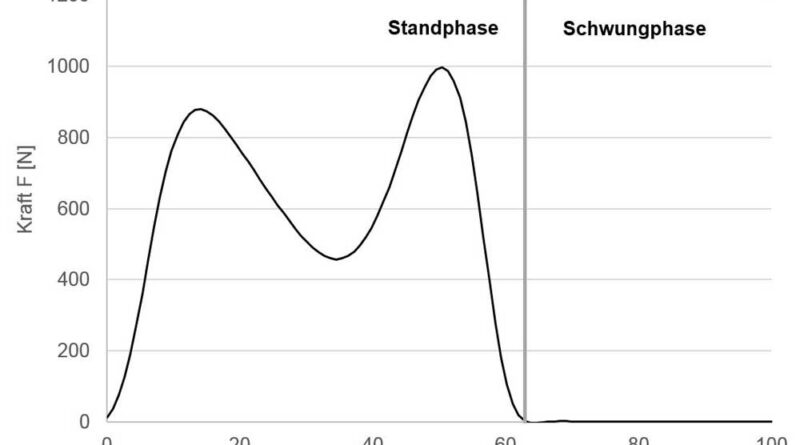
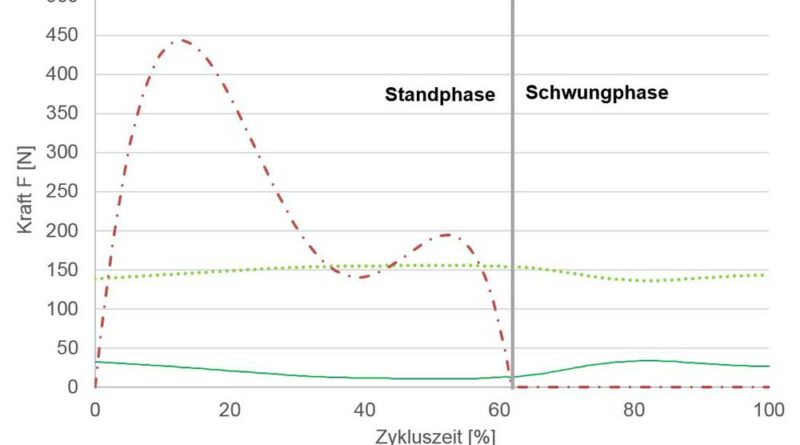
Die kinematischen Daten in Form aufgenommener Markertrajektorien werden implementiert, die realen Marker mit virtuellen Markern gefittet und eine kinematische Optimierung nach 9 zur Berechnung der Gelenkwinkelverläufe durchgeführt. Das Modell des Menschen, mit der die kinematische Berechnung erfolgt, ist mit den aufgenommenen Markertrajektorien in Abbildung 4 dargestellt; die berechneten Gelenkwinkelverläufe sind Abbildung 5 zu entnehmen. Um den mathematischen Einfluss der Markerwichtung zu umgehen, wurden alle Marker mit der gleichen Wichtung von eins angenommen. Die kinetischen Messdaten aus Abbildung 6 wurden zeitgleich implementiert und mit einem Tiefpassfilter (2. Ordnung, 5 Hz Butterworth) geglättet. Die gemessene Zykluszeit beträgt 1,11 s. Davon entfallen 0,68 s auf die Standphase und 0,43 s auf die Schwungphase. Die doppelte Standphase wird vernachlässigt.
Implementierung der aktiven und passiven Unterstützung
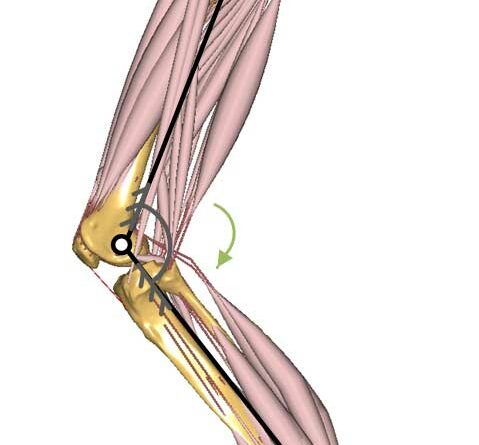
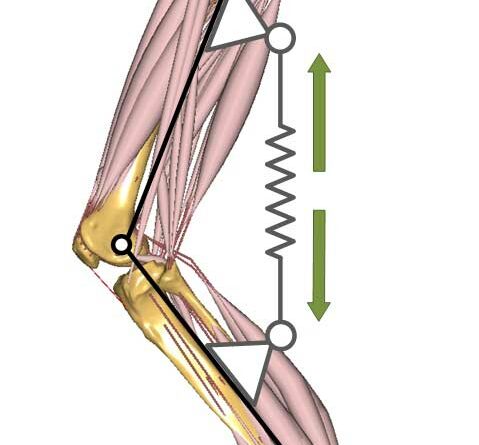
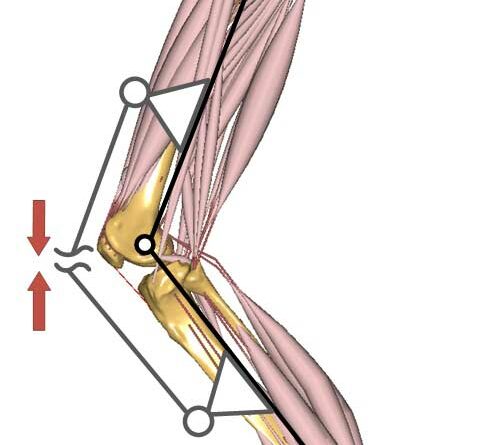
Prinzipiell kann die Knieextension beim Treppenaufstieg durch drei erschiedene Varianten unterstützt werden (Abb. 7):
- Rotationsfeder, die koaxial zur Kniegelenksachse angeordnet ist;
- Translationsfeder, die in posteriorer Lage zwischen Femur und Tibia gespannt ist;
- aktiver Seilzug, der das Kniegelenk anterior überspannt.
Die passive Unterstützung erfolgt durch die Rotations- beziehungsweise Translationsfeder über den gesamten Bewegungszyklus. Die Federkräfte wurden in Abhängigkeit des Kniewinkels implementiert. Die Translationsfeder wurde zum einen in einem Abstand von 0,087 m vom distalen Ende des Femurs an diesen angebunden; zum anderen erfolgte eine Anbindung an die Tibia in einem Abstand von 0,093 m vom proximalen Ende.
Die unterstützende Kraft ist nur in der Standphase aktiv, um den Menschen beim Hochdrücken auf die nächsthöhere Stufe zu unterstützen. In der Schwungphase findet weder eine Unterstützung noch eine Dämpfung statt. Die Verläufe der drei unterstützenden Kräfte, die in den Elementen selbst wirken, ist in Abbildung 8 dargestellt.
Durchführung der Simulation
Da die Bewegung durch die biomechanische Messung bekannt ist, können die für die Bewegung verantwortlichen Muskelkräfte und Momente berechnet werden. Dies erfolgt durch den Ansatz der inversen Dynamik, den die AMS-Software nutzt, um interne Muskelkräfte und ‑momente zu berechnen [10, 11]. Da stets mehrere Muskeln an der Bewegung beteiligt sind, gibt es folglich unendliche viele Lösungen der einzelnen Muskelkräfte. Dieses Problem der Überbestimmtheit wird in AMS durch ein mathematisches Optimierungsverfahren gelöst, in dem die Gesamtbelastung aller an der Bewegung beteiligten Muskeln des menschlichen Körpers minimiert wird. Bei dieser Berechnung wird der Einfluss der implementierten unterstützenden Kräfte entsprechend berücksichtigt.
Der Beginn eines Zyklus wurde mit dem ersten Fußkontakt auf der Kraftmessplatte definiert. Die Standphase des betrachteten Beines endet beim Lösen des Kontaktes; gleichzeitig beginnt die Schwungphase. Das Ende der Schwungphase wurde über die kinematischen Daten ermittelt.
Die vergleichende Analyse erfolgt anhand der berechneten Gelenkmomentverläufe der Knieextension ohne und mit Unterstützung durch Rotationsfedern, Translationsfedern und des aktiven Seilzuges (Motor).
Ergebnisse
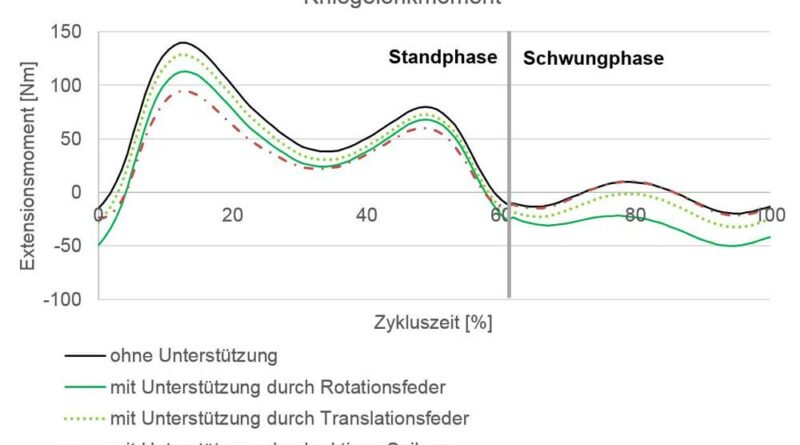
Es können die vom Menschen aufzubringenden Gelenkmomente im Knie während der Stand- und Schwungphase eines Treppenaufstieges jeweils ohne Unterstützung, mit passiver Unterstützung durch Rotations- und Translationsfedern sowie mit aktiver Unterstützung durch den Seilzug (Motor) dargestellt werden (Abb. 9). Die doppelte Standphase wird auch hier vernachlässigt.
In der Standphase kommt es zur Gewichtsakzeptanz sowie zum einbeinigen Hochdrücken des gesamten Körpers. Der Momentenverlauf ohne Unterstützung weist in dieser Phase zwei Peaks auf. Beim Übergang von der Stand- in die Schwungphase geht der Verlauf von einem positiven in einen negativen Bereich über. In der Schwungphase gibt es keine signifikanten Peaks, da in dieser Phase lediglich die Masse der im Schwung befindlichen Unterschenkel- und Fußsegmente Einfluss auf das Kniegelenkmoment hat. Der erste Peak der Standphase erreicht das Maximum von 140 Nm nach ca. 10 % der gesamten Zykluszeit. Bei 50 % der Zykluszeit tritt beim zweiten Peak ein Wert von 80 Nm auf. Der qualitative Verlauf des Kniegelenkmomentes ist für alle Verläufe in der Standphase identisch. Der erste Peak kann durch eine Translationsfeder um 11 Nm, durch eine Rotationsfeder um 27 Nm und durch den aktiven Seilzug um 45 Nm reduziert werden. Der zweite Peak wird durch die Translationsfeder um 12 Nm, durch die Rotationsfeder um 7 Nm und durch den aktiven Seilzug (Motor) um 20 Nm reduziert. In der Schwungphase bleibt der Verlauf bei dem Einsatz der aktiven Unterstützung unverändert. Dagegen ändert sich der quantitative Momentenverlauf durch die passiven Elemente: durch die Rotationsfeder um 33 Nm und durch die Translationsfedern um 11 Nm.
Schlussfolgerung
Sowohl passive als auch aktive Unterstützungsmöglichkeiten können das vom Menschen aufzubringende Gelenkmoment im Knie verringern. Durch eine aktive Unterstützung kann eine Verringerung um bis zu 48 % im ersten und um 32 % im zweiten Peak erreicht werden. Durch die passive Unterstützung ist eine vergleichsweise geringere Reduzierung des ersten Peaks um 23 % und des zweiten Peaks um 17 % möglich. Die passiven Elemente setzen die Gelenkmomente in der Standphase auf Kosten der Schwungphase herab. Im Durchschnitt kommt es in der Schwungphase bei der Translationsfeder zu einer Vergrößerung des Kniegelenkmoments um 89 %, bei der Rotationsfeder um 160 %. Je stärker eine Feder in der Standphase unterstützt, desto stärker muss sie auch in der Schwungphase gespannt werden. Dies könnte wiederum zu unnatürlichen Bewegungsabläufen in der Schwungphase führen. Somit ist für eine reine Unterstützung des Extensionsmomentes im Knie beim Treppenaufstieg die aktive Variante gegenüber der passiven besser geeignet.
Die Rotationsfeder hat im Vergleich zur Translationsfeder nach Abbildung 8 zwar einen betragsmäßig geringeren Kraftverlauf, unterstützt das Kniegelenkmoment aber stärker, da es direkt im Kniegelenk angreift. Demnach kann geschlussfolgert werden, dass nicht der Kraftverlauf im Element alleine für eine Unterstützung entscheidend ist, sondern auch der vektorielle Anteil der Kraft, der zu einem unterstützenden Drehmoment führt. Somit sind Kraftangriffspunkte ebenso entscheidend wie der Kraftverlauf selbst.
Fazit
Biomechanische Simulationen bieten prinzipiell ein enormes Potenzial, um die Entwicklung orthetischer Systeme zielsicherer sowie zeit- und ressourceneffizienter zu gestalten. Mit ihrer Hilfe ist es möglich, bereits in frühen Entwicklungsphasen, wenn das potenzielle Produkt erst als funktionelle oder prinzipielle Lösung vorliegt, diese am Menschen und in Wechselwirkung mit dessen Bewegungsapparat mittels Simulationen funktionell abzusichern und strukturell zu optimieren.
Für das im Mittelpunkt dieser Arbeit stehende Bewegungsunterstützungssystem wurden drei verschiedene prinzipielle Lösungen untersucht, indem sie in Wechselwirkung mit dem Menschen simuliert wurden. Es konnte gezeigt werden, dass durch aktive Unterstützung eine Verringerung der vom Menschen aufzubringenden Kraft um bis zu 48 % im ersten und um 32 % im zweiten Peak erreicht werden kann. Auf der anderen Seite wurde ermittelt, dass mit der passiven Unterstützung, die im Vorfeld durchaus positiv gesehen wurde, zwar in der Standphase ebenfalls eine signifikante Verringerung der aufzubringenden Kraft erreicht werden kann (23 % und 17 % entsprechend), dass dies aber mit einem im Verhältnis immensen Anstieg der aufzubringenden Kraft (89 % und 160 %) in der Schwungphase erkauft wird. Durch die solide begründete Weiterverfolgung der prinzipiellen Lösung mit aktiver Unterstützung wurde die Produktentwicklung frühzeitig auf den Weg mit höchster Erfolgswahrscheinlichkeit gelenkt.
Der Autor:
Max Böhme M. Eng.
Wissenschaftlicher Mitarbeiter
Fakultät Ingenieurwissenschaften
Hochschule für Technik,
Wirtschaft und Kultur Leipzig
Karl-Liebknecht-Str. 132
04277 Leipzig
max.boehme@htwk-leipzig.de
Begutachteter Beitrag/Reviewed paper
Böhme M, Zentner J. Biomechanische Simulation orthetischer Teilsysteme in der Entwurfsphase. Orthopädie Technik, 2020; 71 (9): 44–48
- Kinder mit Trisomie 21: Einsatz der Ganganalyse zur adäquaten Schuh- und Orthesenversorgung — 5. November 2024
- Rehabilitation aus orthopädietechnischer und physiotherapeutischer Sicht – Osseointegration und Schaftprothesen der unteren Extremität im Vergleich — 5. November 2024
- Belastungsprofile von knochenverankerten Oberschenkelimplantaten verbunden mit modernen Prothesenpassteilen — 5. November 2024
- Winter DA. Biomechanics and motor control of human movement. Hoboken, N. J.: Wiley, 2009
- Damsgaard M, Rasmussen J, Christensen ST, Surma E, de Zee M. Analysis of musculoskeletal systems in the AnyBody Modeling
System. Simulation Modelling Practice and Theory, 2006; 14: 1100–1111 - Kluess D, Hurschler C, Voigt C, Hölzer A, Stoffel M. Einsatzgebiete der numerischen Simulation in der muskuloskelettalen Forschung und ihre Bedeutung für die Orthopädische Chirurgie. Der Orthopäde, 2013; 42: 220–231
- Deutsches Institut für Normung e. V. DIN 18065:2020–08. Gebäudetreppen – Begriffe, Messregeln, Hauptmaße. Ausgabedatum: 2015-03. Berlin: Beuth Verlag, 2015
- Cappozzo A, Catani F, Della Croce U, Leardini A. Position and orientation in space of bones during movement: anatomical frame definition and determination. Clinical Biomechanics, 1995; 10: 171–178
- Klein Horsman MD. The Twente lower extremity model. Consistent dynamic simulation of the human locomotor apparatus. Dissertation, Universiteit Twente, Enschede, 2007. https://ris.utwente.nl/ws/portalfiles/portal/6069748/thesis__Klein_Horsman. pdf (Zugriff am 31.07.2020)
- Rasmussen J, de Zee M, Damsgaard M, Christensen ST, Marek K, Siebertz K. A General Method for Scaling Musculo-Skeletal Models. 2005 International Symposium on Computer Simulation in Biomechanics, Cleveland, Ohio (USA)
- C‑MotionWiki Documentation. Coda Pelvis. https://www.c‑motion.com/v3dwiki/index.php?title=Coda_Pelvis (Zugriff am 31.07.2020)
- Andersen MS, Damsgaard M, MacWilliams B, Rasmussen J. A computationally efficient optimisation-based method for parameter identification of kinematically determinate and over-determinate biomechanical systems. Computer Methods in Biomechanics and Biomedical Engineering, 2010; 13: 171–183