Stand der Technik
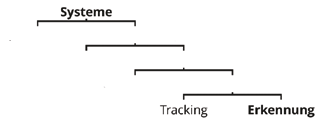
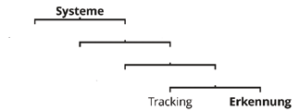
Um das neue Verfahren einordnen zu können, werden zunächst die verschiedenen Klassen von Bewegungsanalysesystemen vorgestellt. Abbilung 1 zeigt ihre Struktur zur besseren Orientierung auf:
Markerlose Systeme
Bei markerlosen Systemen wird ein Patient gleichzeitig aus vielen verschiedenen Perspektiven gefilmt. Dafür werden ca. 10 bis 20 Kameras und ein einfarbiger, gut ausgeleuchteter Raum benötigt, in dem sich nur der Patient befindet. Aus den 16 simultanen Aufnahmen wird das Volumen des Patienten berechnet. Man kann sich das Volumen als ein 3D-Foto eines Menschen vorstellen. Statt eines Pixels (2D-Quadrat) besteht diese Aufnahme aus vielen kleinen Würfeln („Voxel” = „Volume Pixel”). Diese Aufnahme lässt sich aber noch nicht für eine Bewegungsanalyse nutzen, die auf biometrischen Parametern beruht.
In einem weiteren Schritt muss deshalb die Pose eines Mensch-Modells geschätzt werden, die sich mit dem Volumen deckt. Die Präzision dieses Schrittes ist mittelmäßig. Eine weitere Einschränkung bringt die Volumenberechnung mit sich, für die in der Regel das sogenannte Space-Carving-Verfahren 1 („space carving” zu Deutsch wörtlich „Raumschnitzen”) verwendet wird. Bildlich gesprochen können mit diesem Verfahren nur Volumen dargestellt werden, die sich mit einer Laubsäge fertigen ließen, Löcher und Rillen verschwinden also. Demonstrationsvideos zeigen deshalb häufig Kampfsportler, die breitbeinig stehen und die Arme weit abspreizen. Bei anliegenden Extremitäten würden diese nämlich mit dem Körper verschmelzen und könnten im zweiten Schritt deshalb schlecht identifiziert werden.
Streifenlichtprojektion
Ein weiteres markerloses System, das kurz erwähnt werden sollte, ist die Streifenlichtprojektion 2. Dabei wird eine Folge von Streifenmustern auf einen Gegenstand projiziert und von einer Kamera aus einer anderen Perspektive gefilmt. Aus der Verzerrung der Streifen auf dem Gegenstand wird die Entfernung berechnet. Es ergibt sich so ein 2,5‑D-Bild, das einer Höhenkarte entspricht. Man erhält also nur Informationen von einer Seite des Patienten.
Systeme mit Markern
Bei markerbasierten Systemen werden Marker am Körper des Patienten angebracht. In der Regel werden sie auf anatomische Referenzpunkte geklebt, die durch Palpation ermittelt werden. Durch die Palpation wird ein Bezug zur Anatomie hergestellt, der markerlosen Systemen verborgen bleibt. Markerbasierte Systeme lassen sich grob in aktive und passive Systeme unterteilen.
Aktive Marker
Bei den aktiven Systemen werden LEDs oder Ultraschallsender am Körper angebracht, die aktiv ein Signal aussenden. Die Systeme bieten den Vorteil einer einfachen Signalverarbeitung, allerdings können die Sensoren durch das Gewicht der Elektronik und der Batterien als störend empfunden werden.
Retroreflexive Marker
Passive Systeme verwenden nur optische Marker. In der Wissenschaft haben sich bisher retroreflexive Marker etabliert, die mit einer speziellen Folie beschichtet sind, die Licht in die Richtung der Quelle zurückwirft. Diesen Effekt kennt man zum Beispiel von Verkehrsschildern. Um ihn zu nutzen, verwenden typische Systeme Infrarotkameras mit ringförmig darum angebrachten Infrarotscheinwerfern (Infrarot-LEDs). Die Marker erscheinen dadurch als sehr helle Punkte in einem ansonsten recht dunklen Bild. Diese Punkte lassen sich durch Software einfach lokalisieren 3. Damit keine Fehlerkennungen entstehen, muss das Bild aber ansonsten dunkel sein. Aufnahmen im Freien oder glänzende Oberflächen (Fußboden) sind problematisch.
Musterbasierte Marker
Bei musterbasierten Systemen werden handelsübliche Kameras und bestimmte Muster wie ein Kreuz oder Kreisring als Marker verwendet. Um solche Muster zu verarbeiten, gibt es zwei Klassen von Verfahren: Tracking (dt. „Verfolgung”) und Erkennung.
Markerverfolgung
Bei der Markerverfolgung (Tracking 4) klickt der Anwender zu Beginn der Aufnahme auf jeden Marker. Diese werden dann von Videobild zu Videobild verfolgt, bis sie nicht mehr sichtbar sind oder sich ihre Darstellung verändert hat. Dazu genügt auch ein kurzfristiges Verdecken durch einen Arm, einen Schatten oder eine Reflexion. In diesem Fall muss der Benutzer die Marker erneut anklicken. Trackingverfahren sind generisch und können mit verschiedenen Mustern als Marker verwendet werden. Allerdings ist stets eine Interaktion des Benutzers notwendig, die erhebliche Arbeitszeit verschlingen kann.
Markererkennung
Ein Erkennungsverfahren hingegen lokalisiert Marker automatisch, also ohne Interaktion des Benutzers. Hierfür wurden bisher Algorithmen verwendet, die eine Vorlage des Markers Pixel für Pixel mit jeder Stelle des Bildes verglichen. Auch dieses Verfahren („Pattern-Matching”) ist recht generisch. Durch den pixelweisen Vergleich ist es allerdings nicht besonders tolerant gegenüber Größenunterschieden, Verzerrungen und Störungen (Schatten, Reflexionen). Die Erkennungsrate hängt daher stark von der Qualität der Aufnahme ab.
Im Folgenden wird ein neues Erkennungsverfahren vorgestellt, das auch bei widrigen Aufnahmebedingungen gute Ergebnisse liefert. Als Marker werden dabei Kreisringe verwendet. Bevor das Verfahren beschrieben wird, soll kurz auf die prinzipiellen Schwierigkeiten der Bildverarbeitung eingegangen werden.
Verfahren zur Markererkennung
Die Schwierigkeiten der Bildverarbeitung
Beim Anlegen eines E‑Mail-Kontos muss man häufig ein paar verzerrte Zahlen abtippen, wie in Abbildung 2 zu sehen. Grund dafür ist die Komplexität der Bildverarbeitung. Menschen können die Zahlen recht gut erkennen, Computer hingegen nicht. Mit der Eingabe beweisen sie, dass sie ein Mensch sind. Der Betreiber schützt sich durch diese sogenannten Captchas vor bösartigen Computer-Programmen, die sonst massenhaft Konten anlegen, um Werbung (Spam) zu verschicken.
Die Erkennung eines Markers ist ein ähnliches Problem. Auf den ersten Blick scheint sie nicht besonders schwierig zu sein. Selbst ein kleines Kind kann diese Aufgabe lösen. Das liegt allerdings daran, dass wir als Menschen sehr gut Bilder analysieren können. So erkennen die meisten in Abbildung 3 nicht vier unabhängige schwarze Flächen, sondern ein schwarzes Kreuz, das mittig von einem hellen Kreis verdeckt wird. Fehlendes wird also automatisch ergänzt. Ebenso werden Reflexionen, Schatten und Verzerrungen unbewusst kompensiert. Optische Täuschungen nutzen dies aus, um eine falsche Wahrnehmung zu provozieren.
Im Gegensatz zu einem Menschen „sieht” ein Computer hingegen nur eine Folge von Zahlen. Abbildung 4 zeigt die vorherige Abbildung als „8-×-8-Pixel-Bild”, wobei der Wert 255 der Farbe Weiß und der Wert 0 der Farbe Schwarz entspricht. Einem Menschen fällt es nun ebenfalls schwer auszurechnen, was hier abgebildet wird.
Bei bisherigen Systemen hat man deshalb versucht, die Probleme der Bildverarbeitung durch zwei Maßnahmen zu umgehen: erstens durch Verwendung von Spezialkameras und besonderen Markern, die als sehr helle Punkte dargestellt werden und deshalb algorithmisch einfach zu lokalisieren sind, zweitens durch Benutzerinteraktion, wodurch die schwierigen Teile der Bildverarbeitung vom Computer auf den Benutzer übertragen werden. Als Benutzer muss man also zwischen hohen Anschaffungskosten für Spezialhardware und hohem Arbeitsaufwand für die Analyse abwägen. Der folgende Algorithmus verfolgt deshalb das Ziel einer automatischen Markererkennung (ohne Interaktion) bei Verwendung handelsüblicher Kameras und simplen Markern.
Marker
Als Marker werden Kreisringe verwendet. Sie sind ein einfaches Muster, das auch bei geringer Auflösung einer Kamera noch gut erkannt werden kann. Auf der anderen Seite trägt es genügend Information, um nicht zufällig in einem Bild enthalten zu sein. Ein Punkt erfüllt dieses Kriterium nicht.
Normalisierung des Bildes
Das Verfahren sucht unabhängig in jedem einzelnen Bild des Videos nach Markern. Abbildung 5 zeigt oben ein Originalbild eines Videos. Durch ein extremes Weitwinkelobjektiv der Kamera (GoPro HD Hero2) ist es stark tonnenförmig verzeichnet. Im ersten Schritt des Verfahrens erzeugt eine Verzeichnungskorrektur 5 daraus ein verzerrungsfreies Bild. Der Effekt lässt sich gut an den Leisten im Hintergrund nachvollziehen. Wie man an den Rändern des Bildes erkennt, ist die Aufnahme aber noch sehr ungleichmäßig ausgeleuchtet. Eine adaptive Helligkeitsanpassung korrigiert dies und erzeugt ein normalisiertes Bild, das sich durch einen guten Kontrast und homogene Helligkeit auszeichnet.
Erkennung der Marker
Auf dieser Grundlage kann nun durch eine Kantendetektion 6 ein Kantenbild berechnet werden. Eine Kante (weiße Linie) ist dabei das Resultat einer starken Farbänderung im Ausgangsbild. Wie die Vergrößerung des Knies zeigt, ergeben sich für einen Marker also zwei Kanten – ein Kreis auf der Innenseite und ein Kreis auf der Außenseite des ursprünglichen Kreisrings.
Diese Kreise (im Allgemeinen Ellipsen) werden durch eine Ellipsendetektion erkannt. Jede Ellipse ist dabei durch den Mittelpunkt, die Radien und die Rotation eindeutig bestimmt. Von nun an wird also nicht mehr mit vielen Pixeln, sondern mit wenigen geometrischen Parametern gerechnet.
Im letzten Schritt, der Markersuche, werden nun Paare von Ellipsen gesucht, die zusammen einen Marker ergeben. Die Ellipsen müssen also bezüglich Mittelpunkt, Ausrichtung und Verhältnis der Radien zueinander passen. Jedes Paar repräsentiert nun einen Marker. Ellipsen, die kein Paar bilden, werden hingegen verworfen. Im Beispiel sind das jene, die sich aus den weißen Punkten auf dem Laufband ergeben.
Markerdatensatz
Der resultierende Markerdatensatz enthält neben den geometrischen Daten auch die Wahrscheinlichkeit für die Erkennung eines tatsächlichen Markers. Bei der Aufnahme eines Markers unter Idealbedingungen liegt diese bei 100 %. Mit steigenden Störungen wie Reflexion, Verdeckung und Verzerrung nimmt die Wahrscheinlichkeit ab. Bei einer geringen Wahrscheinlichkeit kann es sich schließlich auch um andere Gegenstände im Hintergrund handeln, die zufällig eine gewisse Ähnlichkeit mit einem Marker haben. Über einen Schwellwert kann der Anwender so echte Marker von störenden Mustern individuell abgrenzen.
Robustheit der Markererkennung
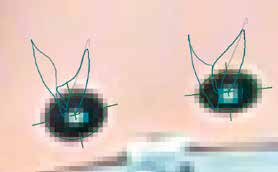
Um die Robustheit des Algorithmus zu überprüfen, wurde die Testszene in Abbildung 6 verwendet. Die Marker in der Szene sind für das menschliche Auge einfach zu erkennen, für einen Algorithmus enthält sie jedoch viele Hürden. So ist zum Beispiel die Bildqualität der 20-Euro-Webcam und die Beleuchtung problematisch. Zudem provozieren störende Muster im Hintergrund Fehlerkennungen.
Wie man sieht, werden sowohl kleine als auch sehr große Marker bei unterschiedlicher perspektivischer Verzerrung zuverlässig erkannt. Das gilt auch bei einer teilweisen Verdeckung eines Markers. Ein gewisses Maß an (Bewegungs-)Unschärfe und Bildrauschen ist ebenso zulässig wie auch andere Verfälschungen. Bei dem Marker im Vordergrund zeigt sich zum Beispiel ein starkes Überschwingen in der Helligkeit am linken und rechten Rand des Kreisringes. Bei genauer Betrachtung sind auch Artefakte durch die Bildkompression der Webcam zu erkennen. Weitere Probleme können durch die Beleuchtung hervorgerufen werden. Der Algorithmus ist deshalb gegenüber Reflexionen auf dem Marker tolerant. Auch kontrastschwache Marker in schlecht ausgeleuchteten Bildern werden erkannt.
Andererseits ist die Rate an Fehlerkennungen sehr gering. Der Algorithmus ist recht robust gegenüber unruhigen Hintergründen und Mustern, wie sie in der Abbildung zahlreich zu sehen sind. So provozieren die weißen Augen des Fisches und das schwarzweiße Blumenmuster im Hintergrund Fehlerkennungen. Der Buchstabe „o” sollte jedoch im Hintergrund vermieden werden, weil er der Definition eines Kreisringes entspricht.
Trajektorienberechnung
Nach der Markererkennung sind für jedes einzelne Standbild die Positionen der Marker bekannt. Für eine Bewegungsanalyse werden aber für jeden Marker Informationen über seine Bewegung benötigt, also seine Position in Abhängigkeit von der Zeit. Diese Ortskurve wird auch als „Trajektorie” bezeichnet. Um sie zu ermitteln, muss die Bewegung des Markers von Videobild zu Videobild verfolgt werden. Für einen Marker lässt sich dieses Problem einfach lösen. Bei mehreren optisch gleichen Markern können jedoch schnell Verwechselungen auftreten. Problematisch ist hier eine geringe Kamerafrequenz bei schnellen Bewegungen und geringen Markerabständen.
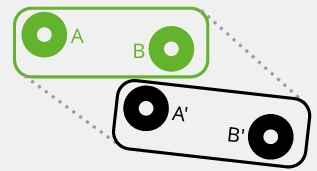
In Abbildung 7 ist ein Beispiel mit zwei Markern zu sehen. Vom ersten Bild (grün) zum zweiten Bild (schwarz) bewegen sich die Marker A und B so weit, dass sich A’ nahe der Position von B befindet. Eine einfache Verfolgung würde deshalb zu dem Fehlschluss kommen, dass sich B nach links unten bewegt hat. Abbildung 8 zeigt ein extremes Anwendungsbeispiel mit 15 dicht beieinanderliegenden Markern auf einer Platte. Die Platte wurde durch den Aufnahmebereich der Kamera geworfen, welche die Bewegung mit einer Frequenz von 50 Hz aufgezeichnet hat. Für die Dauer der betrachteten Flugphase von 0,48 Sekunden ergeben sich so 24 Videobilder. Wie man in Abbildung 9 erkennt, überschreitet der Versatz der Marker zwischen zwei Videobildern (das Folgebild ist blass eingeblendet) deutlich die Abstände zwischen den Markern. Durch ein mehrstufiges Verfahren gelingt es, auch derart schwierige Beispiele zu lösen. Wie man an den parabelförmigen Trajektorien erkennt, werden alle Marker korrekt verfolgt.
Datenanalyse
Die berechneten Trajektorien sind bereits eine gute Grundlage für die Bewertung von Bewegungen. Häufig benötigt der Benutzer aber noch weitere Informationen, die aus den Positionsverläufen mehrerer Marker berechnet werden können. Ein typisches Beispiel ist der zeitliche Verlauf eines Winkels oder die Beschleunigung eines Markers. Solche Datenverarbeitungsprozesse können durch den Benutzer selbst angelegt werden. Ein Prozess kann dann ohne weitere Interaktion für beliebig viele Analysen ausgeführt werden. Dabei werden Marker automatisch benannt, die definierten Berechnungen ausgeführt und ein PDF-Dokument mit den Ergebnissen erzeugt.
Zur Berechnung stehen unter anderem folgende Operationen zur Verfügung:
- Verlauf des Winkels, der durch drei Marker eingeschlossen wird (z. B. Kniewinkel)
- Verlauf des absoluten Winkels zweier Marker (z. B. Winkel zwischen ISG-Markern)
- Verlauf des Abstandes zweier Marker
- Verlauf der x- und y‑Koordinate eines Markers
- zeitliche Ableitung eines beliebigen Verlaufs (z. B. Geschwindigkeit, Beschleunigung)
- Abschätzung der Entfernung eines Markers
- Identifikation von Phasen in einem Verlauf (z. B. Schrittphasen)
- Filterung eines Verlaufs (z. B. Glättung)
Die Operationen können in einem Prozess beliebig häufig verwendet und kombiniert werden.
Beispiel
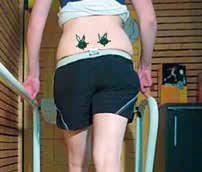
In diesem Beispiel werden zwei ISG-Marker bei normalem Gang betrachtet. Zur Aufzeichnung durfte freundlicherweise das Laufband der Firma Türk in Stuttgart genutzt werden.
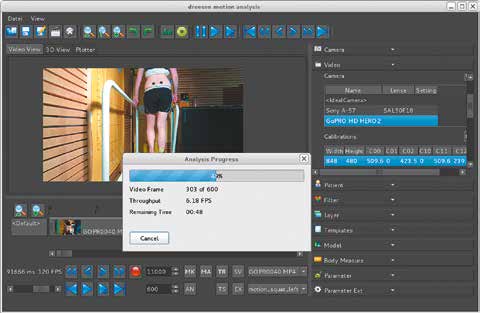
Im Folgenden liegt der Fokus auf dem Analysesystem, also nicht auf medizinischen Aspekten. Abbildung 10 zeigt die automatische Durchführung der Markererkennung. Es wurden 600 vollständige Videobilder in ca. zwei Minuten ausgewertet. Abbildung 11 zeigt das gesamte Videobild mit dem unruhigen Hintergrund. Das Video wurde mit einer Kamera GoPro HD Hero2 aufgezeichnet, die auf eine Aufnahmefrequenz von 120 Hz eingestellt war. Zu sehen ist das Ergebnis der Verzeichnungskorrektur. Abbildung 12 zeigt eine Vergrößerung der Trajektorie für einen Schritt. Obwohl die Kurve nicht gefiltert wurde, hat sie trotz der schlechten Auflösung einen glatten Verlauf mit geringem Rauschen und enthält keinen Ausreißer. Durch den Verzicht auf eine Filterung bleiben auch feinste Verläufe der Trajektorie sichtbar, wie man in der Vergrößerung eines einzelnen Markers in Abbildung 13 gut erkennt.
Die Abbildung demonstriert auch die präzise Berechnung der Markerpositionen trotz geringer Auflösung und unscharfem Bild. Die Markererkennung bestimmt nicht einfach ein Pixel als Mittelpunkt, sondern auch eine Position darin. Diese Eigenschaft nennt man „Subpixel-Genauigkeit”. Die Auflösung der Trajektorie ist also höher als die Auflösung des zugrunde liegenden Videomaterials. Was sich zunächst paradox anhört, lässt sich algorithmisch durch die Berücksichtigung der Pixelfarben erreichen. Wie wertvoll die so gewonnenen Informationen sind, zeigt sich in der folgenden Auswertung: Ohne Subpixel-Genauigkeit spränge die Trajektorie schlagartig von Pixel zu Pixel.
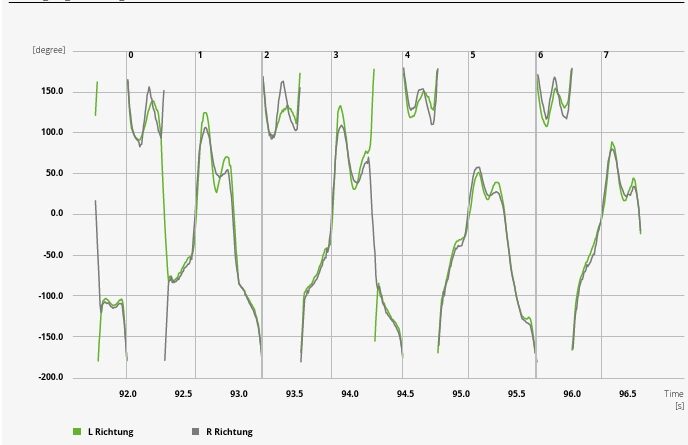
Für die weitere Bearbeitung wurde einmalig ein Analyseprozess definiert, der die folgenden Diagramme erzeugt hat. Das damit erzeugte Diagramm in Abbildung 14 zeigt die Bewegungsrichtung des linken (L) und des rechten ® ISG-Markers, wobei 0° einer Bewegung nach oben, –90° einer Bewegung nach links und +90° einer Bewegung nach rechts entspricht. Sowohl +180° als auch –180° beschreiben eine Bewegung nach unten. Die scheinbar unstetigen Graphen sind durch diese Äquivalenz tatsächlich stetig.
Zusätzlich sind in dem Diagramm durch vertikale Linien die Zeitpunkte markiert, zu denen der Mittelpunkt zwischen L und R vertikal seinen Tiefpunkt erreicht. Das entspricht ungefähr (nicht genau) dem Zeitpunkt des Fersenaufsatzes. Für die gegebene Aufzeichnung decken sich diese Zeitpunkte in etwa mit den Richtungsänderungen von links nach rechts, also einem Durchlauf eines Vielfachen von 180°.
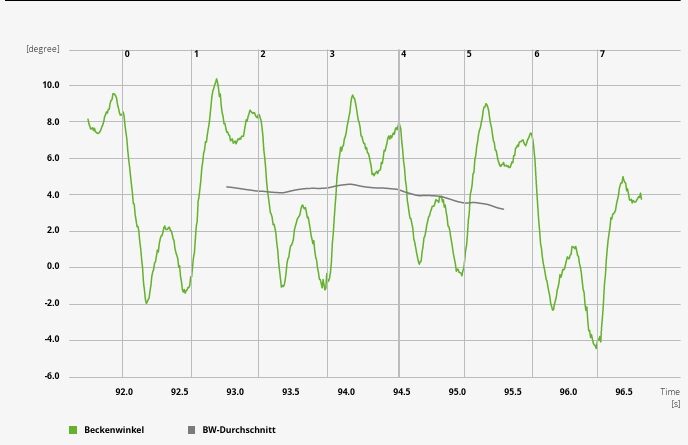
Das Diagramm in Abbildung 15 zeigt den zeitlichen Verlauf des Beckenwinkels auf. Der Beckenwinkel gibt die Rotation der ISG-Marker zur Horizontalen gegen den Uhrzeigersinn an. Ein positiver Winkel beschreibt also eine Kippung nach links und ein negativer Winkel eine Kippung nach rechts.
Obwohl der Verlauf nicht geglättet wurde und die ISG-Marker dicht beieinander liegen (30 Pixel), bewegt sich das Rauschen des Winkels im Bereich von nur 0,2°. Ohne Subpixel-Genauigkeit würde der Winkel hingegen in Schritten von ca. 2° (= atan (1/30)) springen. Die Durchschnittslinie im Diagramm zeigt eine allgemeine Linkskippung des Beckens um 4 °. In den Randbereichen ist der Durchschnitt wegen unzureichender Daten nicht definiert.
Neben diesen Diagrammen wurden noch weitere erzeugt, unter anderem für die Höhe der Marker einschließlich Ableitungen und für die Geschwindigkeit bzw. Beschleunigung der Marker in der Ebene. Der Prozess für die Diagramme wurde in ca. 15 Minuten angelegt. Eine Auswertung damit dauert ca. eine Sekunde.
Zusammenfassung
Durch das vorgestellte Verfahren zur robusten Markererkennung können Bewegungen auch mit günstiger Hardware effizient analysiert werden. So kostet die schnelle 120-Hz-Kamera im letzten Beispiel nur etwa 240 Euro. Die starke Verzeichnung, die man dafür in Kauf nehmen muss, wird durch die Software korrigiert. Das Problem der geringen Auflösung wird durch die subpixelgenaue Markererkennung gelöst. Dank des Verzichts auf Interaktion kann die Markererkennung auch große Mengen an Videos automatisch (z. B. über Nacht) analysieren.
Zusammen mit der automatischen Trajektorienberechnung und einem individuell definierbaren Auswertungsprozess ist der lange Arbeitsablauf einer Bewegungsanalyse weitgehend automatisiert. Mit einem Klick gelangt der Benutzer von einem aufgezeichneten Video zu einem Dokument (PDF) mit den gewünschten Diagrammen. Die Interpretation dieser Daten liegt wieder in der Hand des Anwenders. Prinzipiell ließe sich aber auch dieser Schritt automatisieren.
Der Autor:
Dr. rer. nat. Dipl.-Inf. Ralf Dreesen
Spexarder Bahnhof 2
33334 Gütersloh
motion@dreesen.net
Begutachteter Beitrag/reviewed paper
Dreesen R. Automatisierung der Bewegungsanalyse mit günstiger Hardware. Orthopädie Technik, 2014; 65 (12): 36–43
- Vergleichende Prüfung konventioneller und additiv gefertigter Prothesenschäfte in Anlehnung an DIN EN ISO 10328:2016 — 10. März 2026
- Easypreg – ein Faserverbundwerkstoff zum Tiefziehen — 9. März 2026
- Konservative Versorgung einer adulten Skoliose mit einem modularen Bausatz – ein Versorgungsbeispiel — 6. März 2026
- Kutulakos KN, Seitz SM. A Theory of Shape by Space Carving. International Journal of Computer Vision, 2000; 38 (3): 199–218
- Hall-Holt O, Rusinkiewicz S. Stripe boundary codes for real-time structured-light range scanning of moving objects. Proceedings of Computer Vision (ICCV), 2001: 13–19, http://www.cs.princeton.edu/~smr/papers/realtimerange/realtimerange.pdf
- Dorfmüller K. Robust tracking for augmented reality using retroreflective markers. Computers & Graphics, 1999; 23 (6): 795–800
- Szeliski R. Computer Vision: Algorithms and Applications. London: Springer, 2011
- Weng J, Cohen P, Herniou M. Camera calibration with distortion models and accuracy evaluation. Pattern Analysis and Machine Intelligence, 1992; 14 (10): 965–980
- Ziou D, Tabbone S. Edge detection techniques: An overview. International Journal of Pattern Recognition and Image Analysis, 1998; 8 (4): 537–559