1. Einführung
Für eine adäquate Optimierung von Schuhen ist die Kenntnis der sich im Inneren der Körperstrukturen während einer Bewegung (etwa dem Abrollvorgang beim Gehen oder Rennen) abspielenden Mechanismen und der auftretenden mechanischen Belastungen in den Weichgeweberegionen eine Conditio sine qua non. Der menschliche Körper ist ein hochkomplexes System, wobei während einer Bewegung zusätzlich viele Mechanismen von verschiedenen Strukturen einander bedingen und in ständiger Interaktion miteinander stehen. Deswegen sind für eine realistische Einschätzung von im Körper auftretender Belastungen (Kräfte, Momente, Spannungen) während eines dynamischen Bewegungsablaufes geeignete in vivo-Versuche an Probanden unverzichtbar. Es existieren zwar bereits vereinzelte Methoden, um dies zu bewerkstelligen, jedoch sind diese meist mit massiven invasiven Eingriffen am menschlichen Körper verbunden 1. Weiterhin sind die gewonnenen Daten meist nur auf ein lokales Gebiet begrenzt und somit für aussagekräftige Analysen nur in eingeschränktem Maße verwertbar.
Das BOSS-Verfahren 2 3 4 ist nun in der Lage, die vorhandenen Informationslücken zu schließen. Dieses Verfahren basiert auf einer Verknüpfung einer Reihe von Einzelmethoden wie der Magnet-Resonanz Tomographie (MRT) als bildgebendes Verfahren, CAD-Technologien (3D-Rekonstruktion), der klassischen Bewegungsanalyse, in vivo-Materialcharakterisierungen der betroffenen Weichgeweberegionen und der Finite Elemente Methode (FEM) sowie gegebenenfalls der Hinzuziehung einer Mehrkörpersystemsoftware (MKS, etwa AnyBody). Auf Basis dieses sehr umfassenden Verfahrens lassen sich dann auch bei dynamischen Bewegungsabläufen die mechanischen Spannungen in tiefer gelegenen Gewebeschichten bis hin zum Knochen in dreidimensionaler Form darstellen und analysieren.
2. BOSS-Menschmodell für Geh- und Rennvorgänge
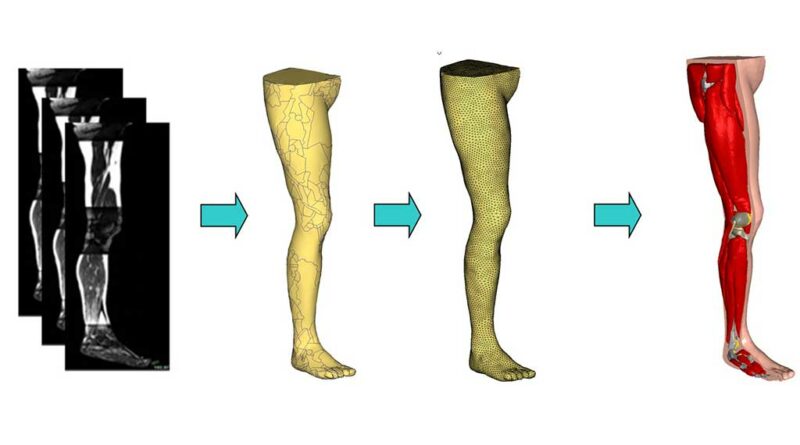
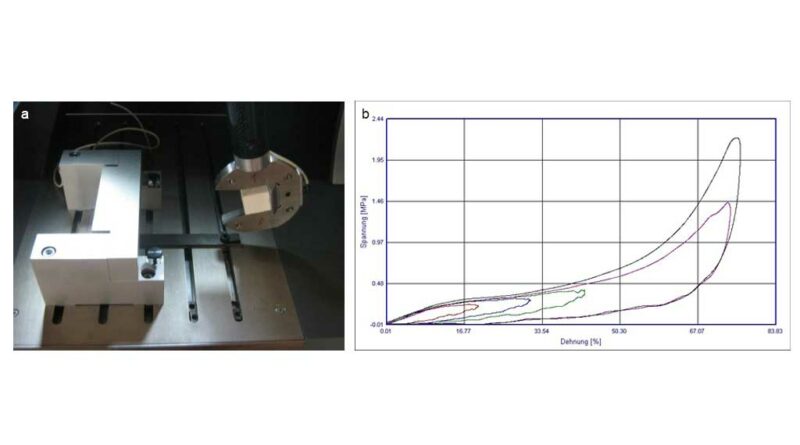
Zur Berechnung der mechanischen Interaktionen zwischen Fuß, Schuh und Untergrund während des Abrollvorganges wurden zunächst Schnittbilder der relevanten Körperregionen (hier einschließlich vom Fuß bis zum Hüftgelenk) an je einem weiblichen und männlichen Probanden mit den folgenden Charakteristika mittels MRT erzeugt (Abb. 1a):
Männlicher Proband:
Alter: 35 Jahre
Größe: 183 cm
Gewicht: 75 kg
BMI: 22,4
Weiblicher Proband:
Alter: 25 Jahre
Größe: 181 cm
Gewicht: 67 kg
BMI: 20,5
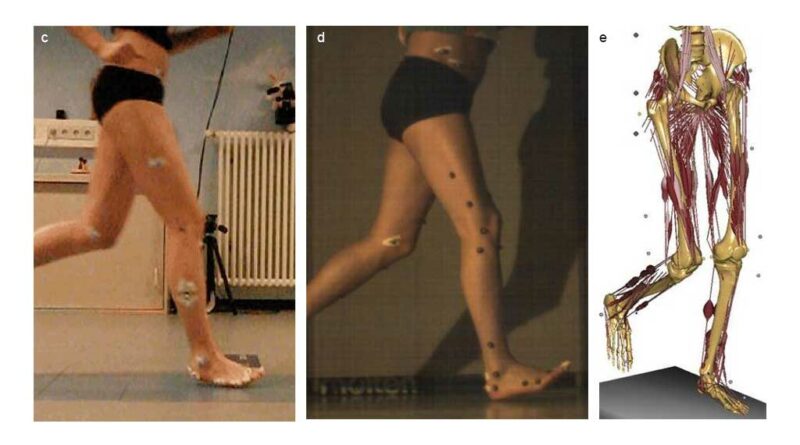
Anschließend erfolgte die Selektion der unterschiedlichen Gewebearten (Haut/Fettgewebe, Muskeln, Knochen, Sehnen, Bänder und Knorpel) sowie deren Oberflächenrückführung mithilfe von 3D-Rekonstruktionstools, auf deren Basis dann mittels der Finite Elemente Methode (FEM) das digitalisierte Beinmodell generiert werden konnte (Abb. 1b bis d).
3. Experimentelle Befunde
Ganganalyse
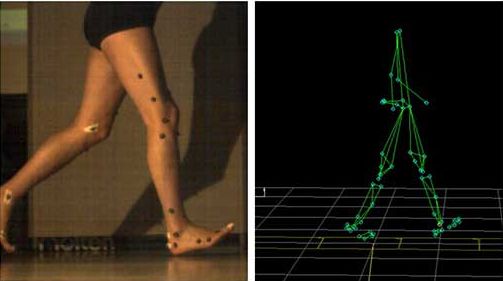
Für die Generierung der Finite Elemente (FE)-Modelle und für die spätere Berechnung der Interaktionen Fuß/Schuh/Unterlage beim Abrollvorgang des Fußes wurden Bewegungsanalysen (Video-High-Speed-Daten) kombiniert mit Bodenreaktionskraftmessungen durchgeführt. Dabei wurden charakteristische Positionen auf der Hautoberfläche des Probanden mit Markern versehen, welche beim Laufen (jeweils barfuß und mit Joggingschuhen mit der Laufgeschwindigkeit von 2,8 m/s) die erforderlichen Signale für die kinematischen Daten lieferten (Abb. 2). Auf Basis der in Form von Human Motion Capture (HMC)-Daten und der gemessenen Bodenreaktionsdruckkräfte erfassten kinematischen und kinetischen Daten erfolgten die späteren numerischen Berechnungen zu den Interaktionen 5.
Dynamische in vivo-Charakterisierung des Fersenpolsters
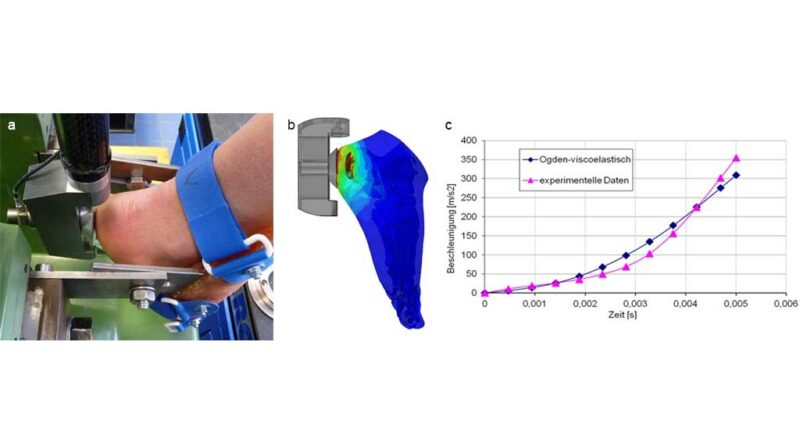
Zur Gewinnung adäquater dynamischer in vivo-Materialeigenschaften des Fersenpolsters der Probanden wurde eine Pendelschlag-Vorrichtung zur Messung der Beschleunigungs-Zeit-Daten beim Impact entwickelt. Um die Elastizität der Fixationsvorrichtung des Fußes und damit möglicherweise verbundene Messfehler minimieren zu können, wurden individuelle Fixationsschalen aus Fiberglas kombiniert mit Edelstahl angefertigt. Auf Basis der Messdaten erfolgte dann mithilfe eines numerischen Optimierungsalgorithmus und der inversen FEM die Identifizierung der dynamischen Materialparameter des Fersenpolsters mittels eines geeigneten Materialgesetzes linear-viskoelastischer nicht-linear-hyperelastischer Materialien (Abb. 3) 6 7 8 9 10 11. Zur Beschreibung der Fettgeweberegionen des Sohlenbereiches und des Fußballens wurden im Rahmen einer ersten Näherung dieselben Materialparameter verwendet.
Materialparameter anderer Weichgewebestrukturen des Fußes
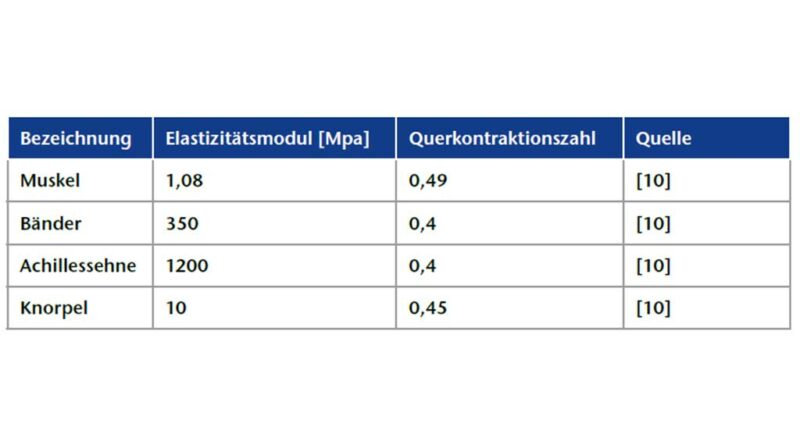
Die weiteren Materialparameter, solche humane Weichgewebestrukturen betreffend wie etwa Bänder, Knorpel, Sehnen und Muskeln, wurden im Rahmen der vorliegenden Betrachtung der einschlägigen Literatur 12 entnommen (Tab. 1). Obwohl das biologische Verhalten von Weichgewebe nach dem Stand von Wissenschaft und Technik a priori viskoelastischer und meistens nicht-linear elastischer Natur ist, konnten keine dieses Verhalten abbildenden Materialparameter in der Literatur recherchiert werden. Vielmehr beschränken diese sich lediglich auf linear-elastisches Materialverhalten.
Dynamische Materialcharakterisierung der Sohlenmaterialien
Die Bestimmung der dynamischen Werkstoffkennwerte der zum Einsatz kommenden Sohlenmaterialien erfolgte an quaderförmigen Materialproben (20 x 20 x 20 mm3) im Rahmen von (dynamischen) Impactversuchen bei definierten Klimata (vgl. Abb. 4). Die Durchführung der Versuche erfolgte in Kooperation mit dem Labor für Mechanik (Prof. S. Kolling) der Technischen Hochschule Mittelhessen an der dort vorhandenen Versuchsvorrichtung in Form eines Pendelschlagwerkes. Mithilfe eines im FE-Solver Abaqus implementierten kontinuumsmechanischen Materialgesetzes für dehnungsabhängige Materialien sowie eines numerischen Optimierungsalgorithmus 13 wurden auf Basis der dynamischen experimentellen Befunde (Beschleunigungs-Zeit-Daten) die Materialparameter der Sohlenmaterialien unter der Voraussetzung einer bestmöglichen Abbildung der dynamischen Spannungs-Dehnungs-Daten in Abhängigkeit der Dehnraten identifiziert.
4. Ergebnisse
Berechnung der Achillessehnenkräfte
Mithilfe der Software AnyBody wurden die in der Achillessehne auftretenden Kräfte während der Standphase am Beispiel eines weiblichen und männlichen Probanden jeweils mit Schuh und barfuß berechnet und an die FE-Modelle ausgegeben. Bei AnyBody handelt es sich um eine Mehrkörpersimulations-Software zur Abbildung vor allem der menschlichen Skelettmuskulatur (ohne Berücksichtigung von Weichgewebestrukturen in Form von Fett-Muskel-Verbünden) bei diversen Bewegungszuständen. Die Software ist speziell für die Rückwärtsberechnung (inverse Dynamik) von Gelenkreaktionen und Muskelkräften konzipiert, wobei auf Basis definierter Bewegungsdaten und Randbedingungen des Modellsystems die Bestimmung von Muskelaktivitäten und daraus resultierender Gelenkkräfte ermöglicht wird.
In diesem Programm ist allerdings die Achillessehne nicht direkt implementiert, sondern nur die Sehnen der einzelnen Muskelstränge im Wesentlichen von M. soleus und M. gastrocnemius jeweils lateral und medial, welche am Calcaneus in einem Punkt zusammenlaufen.
Da sich die Dehnungen der einzelnen Muskelstränge voneinander unterscheiden, die Berechnung einer „Gesamt“-Dehnung der Achillessehne infolge der Einzeldehnungen dieser Stränge gemäß der Software jedoch völlig unklar ist, wurde auf deren Berechnung verzichtet.
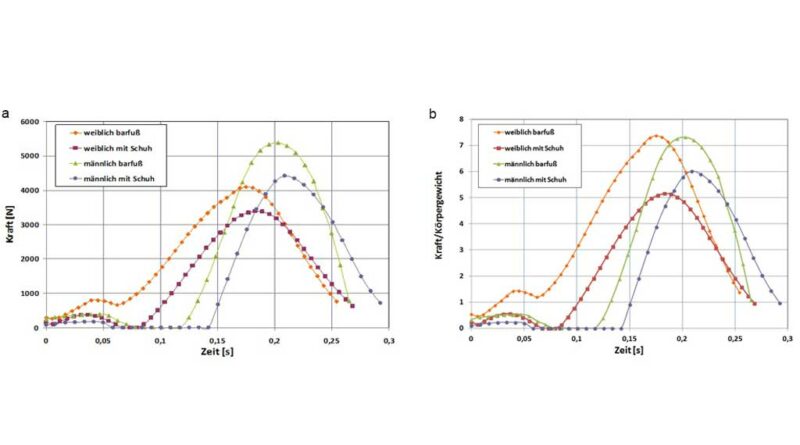
Die maximale Belastung der Achillessehne betrug im Rahmen der vorliegenden Analyse etwa das 7,3‑fache des Körpergewichts der jeweiligen Probanden beim Barfußlauf (Abb. 5a). Darüber hinaus wurde auch die maximale Kraft der Achillessehne bei der Abstoßphase quantifiziert. Bei der Abstoßphase wird die Ferse angehoben und das Bein bewegt sich durch Abrollen über den Vorfuß nach vorne. Während der gesamten Phase befindet sich das Körpergewicht auf dem Vorfuß, wobei dies mit einer hohen Muskelkraft der Achillessehne einhergeht. Anhand von Abbildung 5b ist weiterhin zu erkennen, dass sich der Kraft-Zeit-Verlauf der Achillessehne beim weiblichen Probanden beim Barfußlauf insofern qualitativ abhebt, als dass in der Anfangsphase bei etwa 0,04 s ein Nebenmaximum in Form einer höheren Kraft im Vergleich zu den anderen Kraft-Zeit-Verläufen auftritt. Dies ist durch den Vorfußlaufstil der Probandin erklärbar (Abb. 5c).
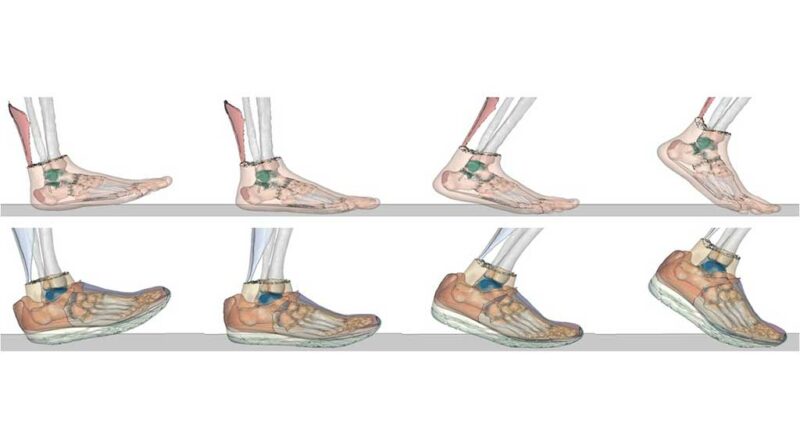
Dynamische Interaktionsberechnungen Fuß/Schuh
Für die FE-Berechnungen der dynamischen Interaktionen zwischen Fuß, Schuh und Untergrund bzw. zwischen Fuß und Untergrund während der Standphase wurde der ABAQUS-Solver „explicit“ angewandt. Hierzu wurden die aus den Ganganalysen gewonnenen kinetischen und kinematischen Daten, die Materialparameter aller Komponenten sowie die mithilfe der AnyBody-Software berechneten Achillessehnenkräfte den FE-Modellen zugeordnet. Die Auswertung der Ergebnisse fokussiert auf die mechanischen Spannungen in der Achillessehne und im Fersenpolster, sodass aus Gründen möglichst kleiner Rechenzeiten die im FE-Beinmodell enthaltenen Knochen in vereinfachter Weise als Starrelemente definiert wurden. Eine weitere Vereinfachung der FE-Modelle erfolgte durch die Entfernung der Muskel- und Fettgewebe in den Unterschenkel- und Oberschenkelregionen.
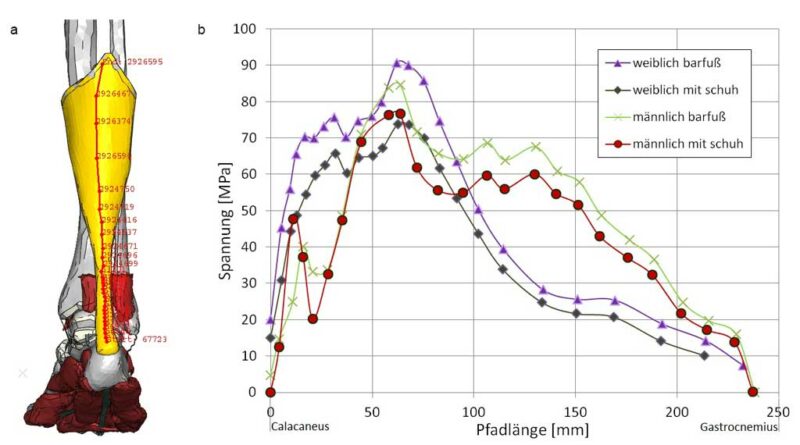
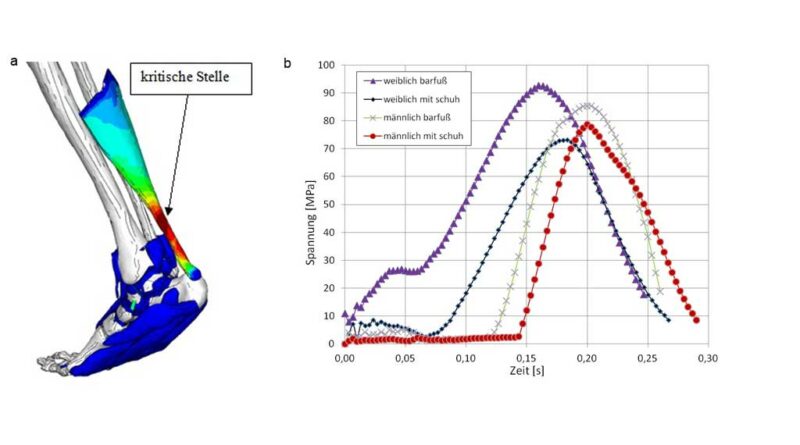
Um die Spannungen im Inneren der Achillessehne aufdecken zu können, wurde ein Knotenpfad von der Insertion am Calcaneus bis zum Gastrocnemius definiert (Abb. 7a). Hierbei wurde die von MISES-Spannung*) aller FE-Modelle bei maximaler Achillessehnenkraft in einem Diagramm dargestellt (Abb. 7b). Die maximalen Spannungen aller FE-Modelle treten etwa 60 mm oberhalb der Insertion der Achillessehne am minimalen Querschnitt auf (in vielen Publikationen als „kritische Stelle“ bezeichnet) (Abb. 8a). Es ist festzustellen, dass, obwohl die Kräfte in der Achillessehne beim weiblichen FE-Modell kleiner als diejenigen beim männlichen Modell sind, die Spannungen an der kritischen Stelle des weiblichen Achillessehnenmodells größer sind (siehe Abb. 7b). Dies kann einerseits auf die kleinere Querschnittfläche der weiblichen Achillessehne mit 46 mm2 im Vergleich zur männlichen Achillessehne mit 55 mm2 und andererseits auf den Laufstil der Probandin mit leichter Überpronation zurückgeführt werden.
Darüber hinaus wurde an der kritischen Stelle der Achillessehne dasjenige Finite Element mit der größten Spannung ausgewählt und die Spannung über die Zeit dargestellt (Abb. 8b). Dabei ist ersichtlich, dass die Spannungs-Zeit-Verläufe bei allen FE-Modellen mit den Achillessehnen-Kraft-Zeit-Verläufen des jeweiligen Modells in qualitativer Hinsicht sehr ähnlich sind. Erwartungsgemäß tritt hier die maximale Spannung der Achillessehne während der Abstoßphase auf. Betrachtet man die weiblichen und männlichen Modelle separat, weisen diese Modelle beim Abrollvorgang mit Schuh eine niedrigere Spannung als beim Barfußlauf aus (Abb. 8b).
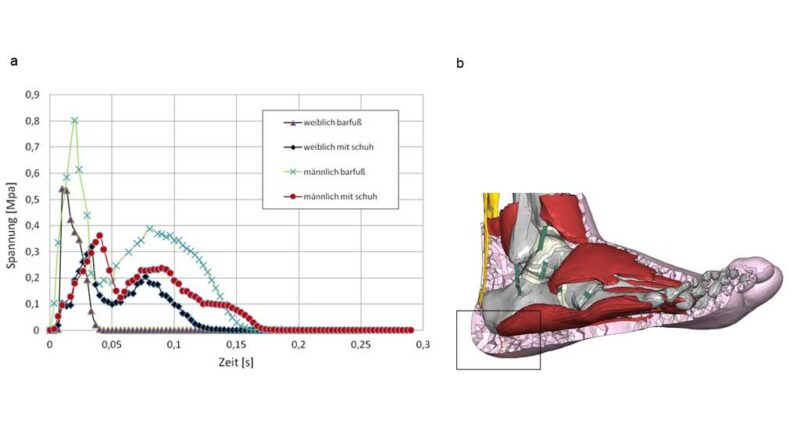
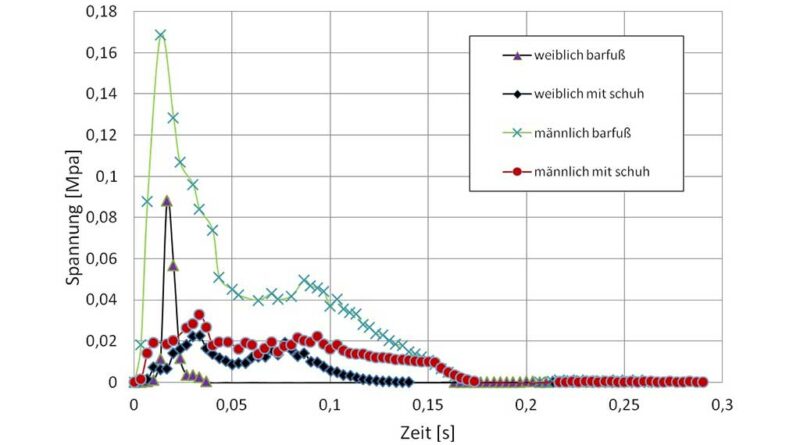
Als ein weiteres Kriterium zur Beurteilung des Laufschuhs wurden die Spannungsverteilungen im Fersenpolster herangezogen. Abbildung 9a bzw. Abbildung 10 zeigen die von MISES-Spannungen bzw. die Scherspannung S23 über die Zeit an dasjenige Finite Element mit der größten Spannung im Fersenpolster. Hierbei ist ein deutlicher Spannungsunterschied zwischen dem Barfuß-Modell und dem Modell mit Schuh zu erkennen. Da der Laufstil des männlichen Probanden durch einen Fersenlauf gekennzeichnet ist, tritt erwartungsgemäß die größte Spannung im Fersenpolster beim männlichen Barfuß-Modell auf. Die Spannungsentwicklung in Abhängigkeit der Zeit deutet darauf hin, dass bei den Barfuß-Modellen während der Belastungsantwort etwa zum Zeitpunkt t = 0,02 s die Spannungsspitze entsteht. Dagegen tritt die Spannungsspitze bei Modellen mit Schuh etwas später, etwa zum Zeitpunkt t = 0,04 s mit geringeren Spannungswerten, auf, was möglicherweise auf die Dämpfungseigenschaften der Sohle zurückzuführen ist.
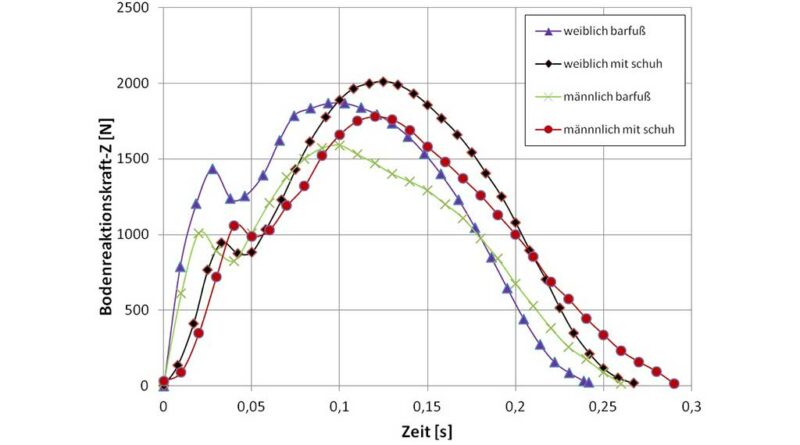
Der Vergleich der Spannungsspitzen im Fersenpolster mit den jeweiligen Bodenreaktionskräften (Abb. 11) zeigt deutlich, dass die maximalen Spannungen zu den Zeitpunkten der maximalen Bodenreaktionskräfte während der Belastungsantwort (erste Kraftspitze) auftreten, allerdings mit Ausnahme des weiblichen Barfuß-Modells, was wieder auf den Vorfußlauf zurückgeführt werden kann. Die Modellrechnungen mit Schuhen zeigen eine deutliche Spannungsreduzierung gegenüber den Barfuß-Modellen. Dieses Phänomen lässt sich durch die passende und optimierte Form des Schuhs zur Fußsohle und die Dämpfung des Aufprallstoßes der Schuhsohle erklären.
5. Resümee
Die bislang zum Einsatz kommenden Methoden zur Gestaltung von Schuhen im Sport- und Rehabereich, wie etwa der Ganganalyse in Kombination mit Drucksensor-Einlegematten, geben keinen Aufschluss über das komplexe dreidimensionale Interaktionsgeschehen zwischen dem menschlichen Bewegungsapparat (insbesondere Fuß) und Schuh bzw. zwischen Fuß und Untergrund. Auf Basis des BOSS-Verfahrens können mithilfe von Probanden erzeugte digitale Menschmodelle mit in vivo-Eigenschaften durch realitätsnahe Computersimulationen erstmalig die infolge der Interaktionen mit einem Schuh entstehenden mechanischen Druck- und Zug- sowie die möglicherweise viel gefährlicheren Scherspannungen sogar in tieferen Gewebeschichten bis hin zum Knochen prinzipiell an jeder beliebigen Stelle im Bewegungsapparat dreidimensional dargestellt („sichtbar“ gemacht) werden. Im Vergleich zu den bisher üblichen Methoden wird das zentrale Potential dieses Verfahrens in der Entwicklung und Optimierung von Schuhen derart liegen können, dass das Interaktionsszenario am Rechner mit Blick auf eine optimale Verletzungsprävention bzw. einen maximalen Komfort solange durchgespielt werden kann, bis Spannungen an gefährdeten anatomischen Stellen (etwa Fersenpolster und Achillessehne) minimiert worden sind. Es ist zu erwarten, dass solche unter Berücksichtigung biomechanisch entwickelter Designvorgaben, vor einer aufwendigen und teuren Fertigung per Simulationen am Rechner gestalteten und dann erst gefertigten Schuhsysteme das Verletzungsrisiko sehr effizient vermindern und/oder den Tragekomfort erhöhen werden.
Die Autoren:
M. Eng. Dipl.-Ing. Majid Kardeh
Fachbereich 2: Informatik und
Ingenieurwissenschaften
kardeh@fb2.fh-frankfurt.de
Prof. Dr.-Ing. habil. Gerhard Silber
Geschäftsführender Direktor des
Instituts für Materialwissenschaften (IfM)
Professur für Materialmodellierung,
Bauteiloptimierung, Kontinuumsmechanik, Materialtheorie
Fachhochschule Frankfurt am Main
- University of Applied Sciences –
Nibelungenplatz 1
60318 Frankfurt
silber@fb2.fh-frankfurt.de
Begutachteter Beitrag/Reviewed paper
* Im Raum existieren im Allgemeinen insgesamt 6 Spannungen (je 3 Normal- und Scherspannungen). Bei der von MISES-Spannung handelt es sich um eine „Vergleichsspannung“ in Form einer einzigen Zahl, welche in bestimmter Weise aus den 6 Normal- und Scherspannungen S11, S22 und S33 und S12, S13 und S23 gebildet wird und insofern sehr oft als „Maß“ für die räumliche Lastsituation herangezogen wird, als dass man nicht mühsam 6 Spannungen analysieren muss.
Kardeh M, Silber G. Biomechanische Optimierung von Schuhen unter Berücksichtigung der Fersenpolster- und Achillessehnenbelastung. Orthopädie Technik, 2013; 64 (7): 54–59
- Vergleichende Prüfung konventioneller und additiv gefertigter Prothesenschäfte in Anlehnung an DIN EN ISO 10328:2016 — 10. März 2026
- Easypreg – ein Faserverbundwerkstoff zum Tiefziehen — 9. März 2026
- Konservative Versorgung einer adulten Skoliose mit einem modularen Bausatz – ein Versorgungsbeispiel — 6. März 2026
- Vogl TJ, Then C, Naguib NN, Nour-Eldin NE, Larson M, Zangos S, Silber G. Mechanical Soft Tissue Property Validation in Tissue Engineering Using Magnetic Resonance Imaging: Experimental Research, Academic Radiology, 2010
- Silber G. Eine neue Methode in der präventiven Biomechanik –Biomechanische Formoptimierung von Liege- und Sitzoberflächen mit Menschmodellen, Orthopädie Technik, 2013; 64 (3): 48–53
- Silber G, Then C. Preventive Biomechanics –Optimizing Support Systems for the Human Body in the Lying and Sitting Position (Lehrbuch), Springer, 2013
- Vogl TJ, Then C, Naguib NN, Nour-Eldin NE, Larson M, Zangos S, Silber G. Mechanical Soft Tissue Property Validation in Tissue Engineering Using Magnetic Resonance Imaging: Experimental Research, Academic Radiology, 2010
- Silva E, Übele K. Finite Elemente Modellierung und numerische Untersuchung der Spannungsverteilung eines Abrollvorganges des Fußes, Bachelorarbeit FH Frankfurt am Main, Institut für Materialwissenschaften, 2011
- Silber G. Ein neuartiges Verfahren zur Gestaltung, Bewertung und Prüfung von Anti-Dekubitus-Systemen, Orthopädie-Technik, 2007; 58 (8): 583–589
- Silber G. Eine neue Methode in der präventiven Biomechanik –Biomechanische Formoptimierung von Liege- und Sitzoberflächen mit Menschmodellen, Orthopädie Technik, 2013; 64 (3): 48–53
- Silva E, Übele K. Finite Elemente Modellierung und numerische Untersuchung der Spannungsverteilung eines Abrollvorganges des Fußes, Bachelorarbeit FH Frankfurt am Main, Institut für Materialwissenschaften, 2011
- Then C, Menger J, Benderoth G, Alizadeh M, Vogl TJ, Hübner F, Silber G. Analysis of mechanical Interaction between human gluteal soft tissue and body supports, Tech Health Care, 2007; 15: 1–16
- Then C, Menger J, Benderoth G, Alizadeh M, Vogl TJ, Hübner F, Silber G. A method for a mechanical characterisation of human gluteal tissue, Tech Health Care, 2007, 15: 385–398
- Then C, Vogl TJ, Silber G. Method for characterizing viscoelasticity of human gluteal tissue, J. of Biomechanics, 2012
- Wu L., Nonlinear finite element analysis for musculoskeletal biomechanics of medial and lateral plantar longitudinal arch of Virtual Chinise Human after plantar ligamentous structure failures, Clinical Biomechanics, 2007; 22: 221–229
- Silber G, Alizadeh M, Salimi M. Large Deformation Analysis for Soft Foams based on Hyperelasticity, Journal of Mechanics 2010; 26 (3): 327–334